��Ŀ����
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱx��h��֮��ĺ���ͼ����ͼ�����������⣺
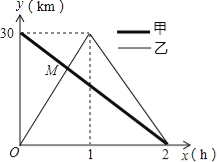
��1��д��A��B����ֱ�ӵľ��룻
��2�������M�����꣬�����õ���������ʾ��ʵ�����壻
��3��������֮�䱣�ֵľ��벻����3kmʱ���ܹ������߶Խ���������ϵ����ֱ��д���ס��������ܹ������߶Խ���������ϵʱx��ȡֵ��Χ��
���𰸡���1��30ǧ�ף���2����M������Ϊ��![]() ��20������ʾ
��20������ʾ![]() Сʱ��������������ʱ����B��20ǧ�ף���3����
Сʱ��������������ʱ����B��20ǧ�ף���3����![]() ��x��
��x��![]() ��
��![]() ��x��2ʱ���ס��������ܹ������߶Խ���������ϵ��
��x��2ʱ���ס��������ܹ������߶Խ���������ϵ��
��������
��1��x=0ʱ��yֵ��ΪA��B���صľ��룻
��2������ͼ������ס������˵��ٶȣ����������������������ʱ�䣬Ȼ������ҵ�·�̼��ɵõ���M�������Լ�ʵ�����壻
��3��������ǰ������������������x��ֵ�������������˶�����B��ǰ�������3ǧ��ʱ�䣬Ȼ��д������ȡֵ��Χ���ɣ�
�⣺��1����x=0ʱ������B��30ǧ�ף�
��A��B���صľ���Ϊ30ǧ�ף�
��2����ͼ��֪�����ٶȣ�30��2=15ǧ��/ʱ���ҵ��ٶȣ�30��1=30ǧ��/ʱ��
30����15+30��=![]() ��
��![]() ��30=20ǧ�ף�
��30=20ǧ�ף�
����M������Ϊ��![]() ��20������ʾ
��20������ʾ![]() Сʱ��������������ʱ����B��20ǧ�ף�
Сʱ��������������ʱ����B��20ǧ�ף�
��3����xСʱʱ���ס����������3km��
����������ǰ����15x+30x=30��3�����x=![]() ��
��
��������������15x+30x=30+3�����x=![]() ��
��
�����ǵ���B��ǰ����15x��30��x��1��=3�����x=![]() ��
��
����![]() ��x��
��x��![]() ��
��![]() ��x��2ʱ���ס��������ܹ������߶Խ���������ϵ��
��x��2ʱ���ס��������ܹ������߶Խ���������ϵ��