题目内容
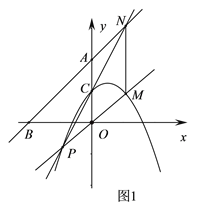
【题目】已知,抛物线y=-![]() x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
(1)直接填写抛物线的解析式________;
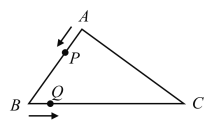
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
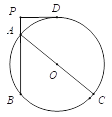
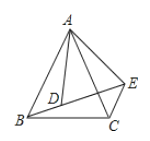
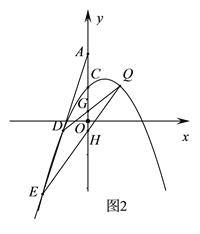
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
【答案】y=-![]() x2+x+2
x2+x+2
【解析】分析:(1)把点C、D代入y=-![]() x2 +bx+c求解即可.
x2 +bx+c求解即可.
(2)分别设PM、PC的解析式,由于PM、PC与抛物线的交点分别为:M、N.,分别求出M、N的代数式即可求解.
(3)先设G、H的坐标,列出QG、GH的解析式,得出与抛物线的交点D、E的横坐标,再列出直线AE的解析式,算出它与抛物线横坐标的交点方程.运用韦达定理即可求证.
详解:(1)∵y=-![]() x2 +bx+c过点C(0,2),点Q(2,2),
x2 +bx+c过点C(0,2),点Q(2,2),
∴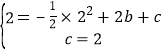 ,解得:
,解得:![]() .
.
∴y=-![]() x2+x+2;
x2+x+2;
(2) 设PM:y=mx,PC:y=kx+2.由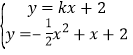 得
得![]() x2+(k-1)x=0,
x2+(k-1)x=0,
xp=![]() .由
.由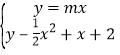 得
得![]() x2+(m-i)x-2=0,xpxm=-4,∴xm=
x2+(m-i)x-2=0,xpxm=-4,∴xm=![]() =
=![]() .
.
由![]() 得xN=
得xN=![]() =xM, ∴MN∥y轴.
=xM, ∴MN∥y轴.
(3)设G(0,m),H(0,n).
得QG:y=![]() x+m,QH:y=
x+m,QH:y=![]() x+n.
x+n.
由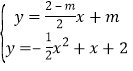 得xD=m-2. 同理得xE=n-2.
得xD=m-2. 同理得xE=n-2.
设AE:y=kx+4,由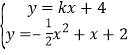 ,得
,得![]() x2-(k-i)x+2=0.
x2-(k-i)x+2=0.
∴xDxE=4,即(m-2)(n-2)=4.
∴CGCH=(2-m)(2-n)=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目