题目内容
 (1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.
(1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.(1)求证:四边形FEHG是矩形;
(2)设FE=x,写出矩形FEHG的面积y与x之间的函数关系式,并指出自变量x的取值范围;
(3)当矩形FEHG的面积是△ABC面积的一半时,两圆的半径有什么关系?并证明你的结论.
分析:(1)要证四边形FEHG为矩形,已知条件有垂直,只需证明四边形为平行四边形,而已知能得出FE与GH平行,只需证FG平行于EH,利用同位角相等两直线平行来证,即要得到∠AGF=∠C,作出两圆的公切线,利用弦切角等于所夹弧所对的圆周角即可得证;
(2)要写出矩形FEHG的面积y与x之间的函数关系式,EF=x,只需用x表示出FG,然后利用矩形的面积公式即可列出;
(3)当矩形FEHG的面积是△ABC面积的一半时,可添加半径,连心线从中找出之间的联系,得出半径间的关系,证明即可.
(2)要写出矩形FEHG的面积y与x之间的函数关系式,EF=x,只需用x表示出FG,然后利用矩形的面积公式即可列出;
(3)当矩形FEHG的面积是△ABC面积的一半时,可添加半径,连心线从中找出之间的联系,得出半径间的关系,证明即可.
解答: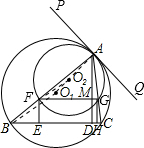 (1)证明:过P作两圆的公切线PQ,如图所示,
(1)证明:过P作两圆的公切线PQ,如图所示,
∴∠PAB=∠AGF,∠PAB=∠C,
∴∠AGF=∠C,
∴FG∥BC,
∵FE⊥BC,GH⊥BC,
∴FE∥GH,
∴四边形FEHG为平行四边形,
∵∠FEC=90°,
则四边形FEHG为矩形;
(2)解:∵FG∥BC,
∴△AFG∽△ABC,
∵AD⊥BC,
∴∠AMG=∠ADC=90°,
∵EF=MD,
∴AM=AD-MD=AD-EF,
∴
=
,
∵EF=x,矩形FEHG面积为y,AD=6,BC=8,
∴
=
,即FG=
(6-x),
则y=
x(6-x)=-
x2+8x(0<x<6);
(3)解:∵S△ABC=
AD•BC=24,矩形FEHG的面积是△ABC面积的一半,
∴-
x2+8x=
×24,即(x-3)2=0,
解得:x1=x2=3,
即当矩形FEHG的面积是△ABC面积的一半时,FE=MD=3,则AM=
AD,
证明:连接O2F,O1B,O1A,则O2必然在O1A上,
∵AO1=BO1,∴∠O1AB=∠O1BA,
∵AO2=FO2,∴∠O2AB=∠O2FA,
∴∠O2FA=∠O2BA,
∴FO2∥BO1,
∴
=
=
=
,
则AM=
AD.
 (1)证明:过P作两圆的公切线PQ,如图所示,
(1)证明:过P作两圆的公切线PQ,如图所示,∴∠PAB=∠AGF,∠PAB=∠C,
∴∠AGF=∠C,
∴FG∥BC,
∵FE⊥BC,GH⊥BC,
∴FE∥GH,
∴四边形FEHG为平行四边形,
∵∠FEC=90°,
则四边形FEHG为矩形;
(2)解:∵FG∥BC,
∴△AFG∽△ABC,
∵AD⊥BC,
∴∠AMG=∠ADC=90°,
∵EF=MD,
∴AM=AD-MD=AD-EF,
∴
| FG |
| BC |
| AM |
| AD |
∵EF=x,矩形FEHG面积为y,AD=6,BC=8,
∴
| FG |
| 8 |
| 6-x |
| 6 |
| 4 |
| 3 |
则y=
| 4 |
| 3 |
| 4 |
| 3 |
(3)解:∵S△ABC=
| 1 |
| 2 |
∴-
| 4 |
| 3 |
| 1 |
| 2 |
解得:x1=x2=3,
即当矩形FEHG的面积是△ABC面积的一半时,FE=MD=3,则AM=
| 1 |
| 2 |
证明:连接O2F,O1B,O1A,则O2必然在O1A上,
∵AO1=BO1,∴∠O1AB=∠O1BA,
∵AO2=FO2,∴∠O2AB=∠O2FA,
∴∠O2FA=∠O2BA,
∴FO2∥BO1,
∴
| O2F |
| O1B |
| AF |
| AB |
| AM |
| AD |
| 1 |
| 2 |
则AM=
| 1 |
| 2 |
点评:此题属于圆综合题,涉及的知识有:圆周角定理,切线的性质,相似是三角形的判定与性质,等腰三角形的性质,平行线等分线段定理,是一道综合性较强的压轴题.

练习册系列答案
相关题目
 (1997•山西)如图,CD是⊙O的直径,且CD=6,弦AB⊥CD于P,PD=1,则AB=
(1997•山西)如图,CD是⊙O的直径,且CD=6,弦AB⊥CD于P,PD=1,则AB= (1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法)
(1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法) (1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.
(1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.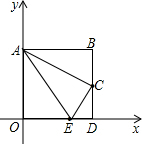 (1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上.
(1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上.