题目内容
 (1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.
(1997•山西)如图,EC是⊙O的直径,且EC=2,作BC⊥AC于C,使BC=2,过B作⊙O的切线BA交CE的延长线于A,切点为D.①求证:AD•AB=AO•AC;
②求AE及AD的长.
分析:①连接CD,易证得△AOD∽△ABC,然后由相似三角形的对应边成比例,证得AD•AB=AO•AC;
②首先设AD=x,AE=y,然后由相似三角形的对应边成比例,得方程
=
,
=
,继而求得答案.
②首先设AD=x,AE=y,然后由相似三角形的对应边成比例,得方程
| x |
| y+2 |
| 1 |
| 2 |
| y+1 |
| x+2 |
| 1 |
| 2 |
解答:①证明: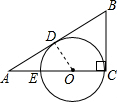 连接OD,
连接OD,
∵AB是⊙O的切线,
∴OD⊥AB,
∴∠ADO=90°,
∵BC⊥AC,
∴∠C=90°,
∴∠ADO=∠C,
∵∠A是公共角,
∴△AOD∽△ABC,
∴AD:AC=AO:AB,
∴AD•AB=AO•AC;
②解:设AD=x,AE=y,
∵EC是⊙O的直径,且EC=2,BC=2,
∴OE=OD=OC=1,
∵△AOD∽△ABC,
∴AD:AC=AO:AB=OD:BC=1:2,
∵AB与BC是⊙O的切线,
∴BD=BC=2,
∴
=
,
=
,
解得:x=
,y=
,
∴AD=
,AE=
.
 连接OD,
连接OD,∵AB是⊙O的切线,
∴OD⊥AB,
∴∠ADO=90°,
∵BC⊥AC,
∴∠C=90°,
∴∠ADO=∠C,
∵∠A是公共角,
∴△AOD∽△ABC,
∴AD:AC=AO:AB,
∴AD•AB=AO•AC;
②解:设AD=x,AE=y,
∵EC是⊙O的直径,且EC=2,BC=2,
∴OE=OD=OC=1,
∵△AOD∽△ABC,
∴AD:AC=AO:AB=OD:BC=1:2,
∵AB与BC是⊙O的切线,
∴BD=BC=2,
∴
| x |
| y+2 |
| 1 |
| 2 |
| y+1 |
| x+2 |
| 1 |
| 2 |
解得:x=
| 4 |
| 3 |
| 2 |
| 3 |
∴AD=
| 4 |
| 3 |
| 2 |
| 3 |
点评:此题考查了切线的性质、相似三角形的判定与性质以及切线长定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 (1997•山西)如图,CD是⊙O的直径,且CD=6,弦AB⊥CD于P,PD=1,则AB=
(1997•山西)如图,CD是⊙O的直径,且CD=6,弦AB⊥CD于P,PD=1,则AB=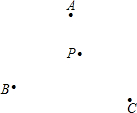 (1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法)
(1997•山西)如图,A、B、C三点表示某平原的三个村庄,要建一个电视转播站,使它到三个村庄的距离相等,求作电视转播站的位置P.(要求:尺规作图,只保留作图痕迹,不写作法)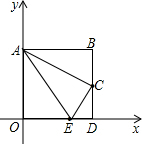 (1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上.
(1997•山西)如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在直线为坐标轴建立直角坐标系,使D、A分别在x轴、y轴的正半轴上. (1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.
(1997•山西)如图,已知△ABC,⊙O1是它的外接圆,与⊙O1内切于A点的⊙O2交AB于F,交AC于G,FE⊥BC于E,GH⊥BC于H,AD是△ABC的高,交FG于M,且AD=6,BC=8.