题目内容
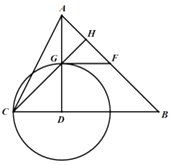
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点. 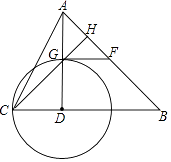
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长.
【答案】
(1)解:∵FG与⊙D相切,
∴∠DGF=90°,
∵AD⊥BC
∴FG∥CB,
∵F为AB中点,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AD=2GD=2CD,
∴tan∠ACD= ![]() =2.
=2.
(2)解:∵AD⊥BC,
∴∠ADB=90°,
∵∠B=45°,
∴△ADB是等腰直角三角形,
∴∠DAB=45°
∵GD=CD,∠GDC=90°,
∴△CGD是等腰直角三角形,
∴∠GCD=45°
∴∠AHC=90°,
∴△AGH是等腰直角三角形,
∵AH=2,
∴HG=2,AG=2 ![]() .
.
∴GD=2 ![]() ,
,
∴CG=4,
∴HC=6,
∴AC= ![]() =2
=2 ![]() .
.
【解析】(1)只要证明AD=2CD即可解决问题;(2)只要证明:△ADB,△CGD,△AGH都是等腰直角三角形,利用等腰三角形的性质即可解决问题;
【考点精析】认真审题,首先需要了解直角三角形斜边上的中线(直角三角形斜边上的中线等于斜边的一半),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数