题目内容
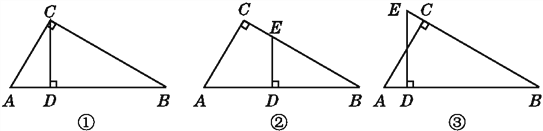
【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.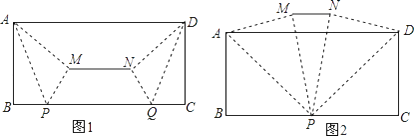
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
【答案】
(1)解:①∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD.
∵在△ABP和△DCQ中,
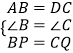 ,
,
∴△ABP≌△DCQ,
∴∠APB=∠DQG.
∴∠MPE=180°﹣2∠APB=180°﹣2∠DQC=∠NQF.
∴在△MEP和△NPQ中,
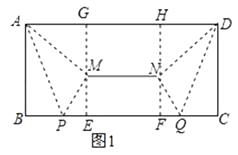
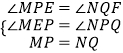 ,
,
∴△MEP≌△NPQ,
∴ME=NF;
②∵ME∥NF,ME=NF,
∴四边形EFMN是矩形,
∴MN∥BC
(2)解:延长EM、FN交AD于点G、H.
∵AB=4,BP=3,
∴AM=4,PM=3.
∵AD∥BC,
∴EM⊥AD.
∵∠AMP=∠MEP=∠MGA,
∴∠EMP=∠MAG.
∴△EMP∽△MAG.
∴ ![]() ,
,
设AG=4a,MG=3b.
∵四边形ABEG是矩形,
∴ ![]() ,
,
解得: 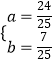 c,
c,
∴AG= ![]() ,同理DH=
,同理DH= ![]() .
.
∴MN= ![]()
(3)解:设PM、PN分别交AD于点E、F.
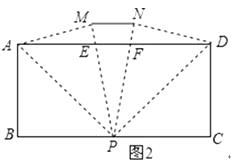
∵∠EPA=∠APB=∠PAE,
∴EA=EP.
设EA=EP=x,
在直角△AME中,42+(6﹣x)2=x2,
解得:x= ![]() .
.
∴EF=12﹣2× ![]() =
= ![]() .
.
∵EF∥MN,
∴△PEF∽△PMN.
∴ ![]() ,即
,即 ![]() ,
,
解得:MN= ![]()
【解析】(1)根据矩形的性质,四边形ABCD是矩形,得到对边相等,四角都是90°,得到△ABP≌△DCQ,△MEP≌△NPQ,得到ME=NF,MN∥BC;(2)由已知条件得到△EMP∽△MAG,得到比例,求出线段MN的长;(3)根据勾股定理求出EF的长,由EF∥MN,得到△PEF∽△PMN,得到比例,求出MN的值.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.