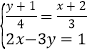题目内容
【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
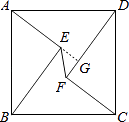
【解析】解:延长AE交DF于G,如图:
∵AB=5,AE=3,BE=4,
∴△ABE是直角三角形,
∴同理可得△DFC是直角三角形,
可得△AGD是直角三角形,
∴∠ABE+∠BAE=∠DAE+∠BAE,
∴∠GAD=∠EBA,
同理可得:∠ADG=∠BAE,
在△AGD和△BAE中,
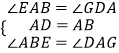 ,
,
∴△AGD≌△BAE(ASA),
∴AG=BE=4,DG=AE=3,
∴EG=4﹣3=1,
同理可得:GF=1,
∴EF= ![]() ,
,
故选D.
【考点精析】利用等腰直角三角形和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目