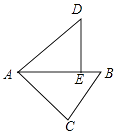Question

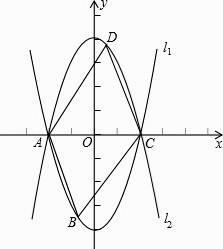
【题目】在平面直角坐标系中，正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上，等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上．

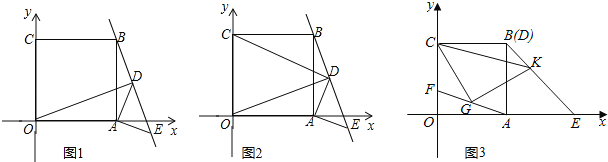
（1）如图1，连接OD，求证：△OAD≌△BAE；

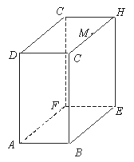
（2）如图2，连接CD，求证：BE﹣DE=CD；

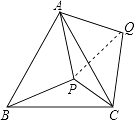
（3）如图3，当图1中的Rt△ADE的顶点D与点B重合时，点E正好落在x轴上，F为线段OC上一动点（不与O、C重合），G为线段AF的中点，若CG⊥GK交BE于点K时，请问∠KCG的大小是否变化？若不变，请求其值；若改变，求出变化的范围．

Answer 1

【答案】（1）证明见解析（2）见解析（3）∠KCG的大小不变，

【解析】

（1）利用同角的余角相等可得∠BAD=∠EAF，由此得∠OAD=∠BAE，根据SAS证明△OAD≌△BAE；（2）作辅助线构建正方形ANDM和等腰直角三角形CFD，把所求CD转化为CF，证CF=OM，由（1）中的全等可知∠ODA=∠BEA=45°，证明∠ODC=45°，推出CF与CD的关系，利用直角三角形斜边中线和正方形的性质求出BE﹣DE的值为OM，得出结论；（3）作辅助线构建正方形BMKN和全等三角形，首先利用全等证明CG=QG，由线段垂直平分线性质得KC=KQ，证明Rt△CNK≌Rt△QMK，得∠CKN=∠QKM，可知∠CKQ=90°，得△KCQ是等腰直角三角形，因此得出结论：∠KCG的大小不变，等于45°．

（1）如图1，在正方形ABCO中，

∵∠BAF=∠DAE=90°，

∴∠BAD=∠EAF，

∴∠BAD+∠OAB=∠EAF+∠BAF，

即∠OAD=∠BAE，

∵AB=AO，AD=AE，

∴△OAD≌△BAE；

（2）如图2，设CD与AB的交点为P，

过C作CF⊥OD于F，过A作AN⊥DE于N，AM⊥OD于M，

∵等腰Rt△ADE，AD=AE，

∴AN=DN=DE，

∴四边形ANDM是正方形，

∴DN=DM，

∴BE﹣DE=OD﹣DM=OM，

由①△OAD≌△BAE得，∠ODA=∠BEA=45°，

∴∠ODE=90°，

∵∠OAB=∠ODB=90°，∠OPA=∠BPD，

∴△OAP∽△BDP，

∴，

∴，

∵∠CBD=90°+∠ABE，∠APD=90°+∠AOD，

∠ABE=∠AOD，

∴∠CBD=∠APD，

∴△CBD∽△APD，

∴∠CDB=∠ADO=45°，

∴∠ODC=90°﹣45°=45°，

∵sin45°=，

∴CF=，

∵△COF≌△OAM，

∴CF=OM，

∴BE﹣DE=CD；

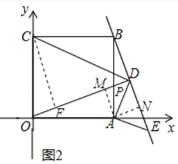
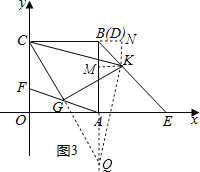
（3）如图3，∠KCG的大小不变，理由是：

过K作KM⊥AB于M，KN⊥BC，交CB的延长线于N，延长CG、BA交于Q，连接KQ，

∵∠N=∠MBN=∠BMK=90°，

∴四边形BMKN是矩形，

∵AB=AE，∠BAE=90°，

∴∠ABE=45°，

∴BM=KM，

∴矩形BMKN是正方形，

∵OC∥AB，

∴∠OCG=∠GQA，

∵FG=AG，∠CGF=∠AGQ，

∴△FCG≌△AQG，

∴CG=QG，

∵CG⊥GK，

∴KC=KQ，

∵KN=KM，

∴Rt△CNK≌Rt△QMK，

∴∠CKN=∠QKM，

∴∠CKQ=∠CKM+∠MKQ=∠CKM+∠CKN=90°，

∴△KCQ是等腰直角三角形，

∴∠KCG=∠KQC=45°．