题目内容
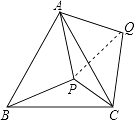
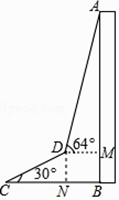
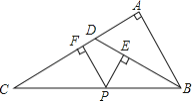
【题目】如图所示，△ABC中，∠A=90°，D是AC上一点，且∠ADB=2∠C，P是BC上任一点，PE⊥BD于点E，PF⊥AC于点F，下列结论：
①△DBC是等腰三角形；②∠C=30°；③PE+PF=AB；④PE2+AF2=BP2．
其中结论正确的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADB=∠C+∠DBC，然后求出∠C=∠DBC，再根据等角对等边可得DC=DB，从而判断①正确；没有条件说明∠C的度数，判断出②错误；连接PD，利用△BCD的面积列式求解即可得到PE+PF=AB，判断出③正确；过点B作BG∥AC交FP的延长线于G，根据两直线平行，内错角相等可得∠C=∠PBG，∠G=∠CFP=90°，然后求出四边形ABGF是矩形，根据矩形的对边相等可得AF=BG，根据然后利用“角角边”证明△BPE和△BPG全等，根据全等三角形对应边相等可得BG=BE，再利用勾股定理列式求解即可判断④正确．
在 △BCD 中， ∠ADB=∠C+∠DBC ，
∵∠ADB=2∠C ，
∴∠C=∠DBC ，
∴DC=DB ，
∴△DBC 是等腰三角形，故①正确；
无法说明 ∠C=30° ，故②错误；
连接 PD ，则 S△BCD=
BDPE+DCPF=DCAB，
∴PE+PF=AB ，故③正确；
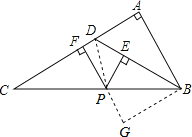
过点 B 作 BG ∥ AC 交 FP 的延长线于 G ，
则 ∠C=∠PBG ， ∠G=∠CFP=90° ，
∴∠PBG=∠DBC ，四边形 ABGF 是矩形，
∴AF=BG ，
在 △BPE 和 △BPG 中，
，
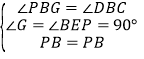∴△BPE ≌ △BPG(AAS) ，
∴BG=BE ，
∴AF=BE ，
在 Rt△PBE 中， PE +BE =BP ，
即 PE +AF =BP ，故④正确。
综上所述，正确的结论有①③④。
故选C.
