��Ŀ����
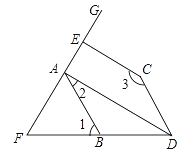
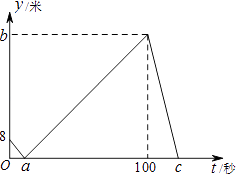
����Ŀ��������С����Ƶġ������ഹֱ������ֱ�ߡ��ij߹���ͼ���̣�
��������ͼ��
����ƽ������ѡһ��O��������OA��OB��
����OΪԲ�ģ������ⳤΪ�뾶�������ֱ�OA�ڵ�C����OB�ڵ�D��
���ֱ���C��DΪԲ�ģ��Դ���![]() CD��ͬ����Ϊ�뾶�������������ڡ�AOB�ڲ�һ��P��
CD��ͬ����Ϊ�뾶�������������ڡ�AOB�ڲ�һ��P��
������CP��PD��
����ֱ��OP����ֱ��CD����ֱ���ཻ�ڵ�E����ֱ��CD��OP�����������Ļ��ഹֱ������ֱ�ߣ�����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������OC���� ����CP���� ����OP��OP
���OPC�ա�OPD
���AOP����BOP��
��OE�ǡ�COD�ĸ��ߣ��� �����������������ݣ�
��OE��CD��
��CD��OP���ഹֱ
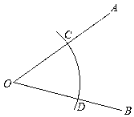
���𰸡���1�������������2��OD��DP���������������ߺ�һ��
��������
��1������Ҫ��ͼ�μ��ɣ�
��2������OPC�ա�OPD��SSS�����Ƴ���AOP����BOP���Ƴ�OE����COD�ĸ����ɽ�����⣻
�⣺��1��ͼ����ͼ��ʾ��
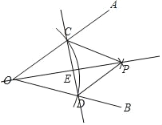
��2�����ɣ���OC��OD��CP��PD��OP��OP��
���OPC�ա�OPD��SSS����
���AOP����BOP��
��OE����COD�ĸ��ߣ��������������ߺ�һ����
��OE��CD��
��CD��OP���ഹֱ��
�ʴ�Ϊ��OD��DP���������������ߺ�һ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�