题目内容
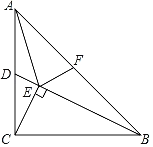
【题目】如图,在![]() 中,
中,![]() 为直径,过点
为直径,过点![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是弦
是弦![]() 延长线上一点,
延长线上一点,![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() ,与
,与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() ,
,![]() .
.
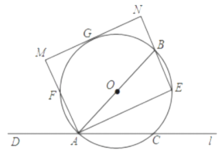
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①13;②![]()
【解析】
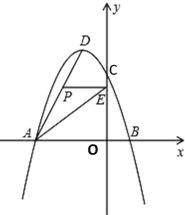
(1)如图1,连接GO、GA,先根据角平分线的定义证明∠MAE=![]() (∠BAC+∠BAD)=90°,由圆周角定理和同圆的半径相等得∠OGA=∠FAG,则OG∥AM,所以∠MGO=180-∠M=90,从而得结论;
(∠BAC+∠BAD)=90°,由圆周角定理和同圆的半径相等得∠OGA=∠FAG,则OG∥AM,所以∠MGO=180-∠M=90,从而得结论;
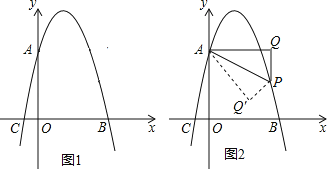
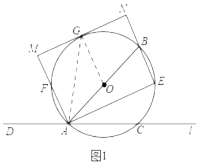
(2)①延长GO交AE于点P,证明四边形MGPA为矩形,得GP=MA=18,∠GPA=90°,设OA=OG=r,则OP=18-r,根据勾股定理列方程解出即可;
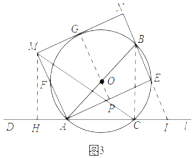
②如图3,过M作MH⊥l,连接BC,延长NE交l于I,连接GO交延长交AE于P,tan∠MAH=tan∠ABE=tan∠BIA=![]() ,BI=2BE=20,根据三角函数计算MH,AH,CI的长,最后计算MH和HC的长,代入tan∠MCD=
,BI=2BE=20,根据三角函数计算MH,AH,CI的长,最后计算MH和HC的长,代入tan∠MCD=![]() ,可得结论.
,可得结论.
(1)证明:如图1,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() 的平分线与
的平分线与![]() 分别相交于点
分别相交于点![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 半径,
半径,
∴![]() 是
是![]() 的切线.
的切线.
(2)解:①如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,

∵![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,即
,即![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
故![]() 的半径是13.
的半径是13.
②如图3,过![]() 作
作![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ,
,
由①知:![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目