题目内容
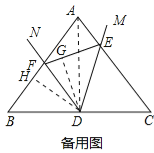
【题目】△ABC中,AB=AC,D为BC的中点,以D为顶点作∠MDN=∠B.

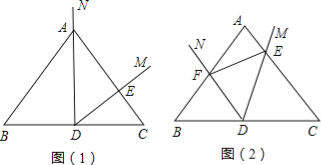
(1)如图(1)当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似的三角形.
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF的面积等于△ABC的面积的![]() 时,求线段EF的长.
时,求线段EF的长.
【答案】(1)见解析 (2)见解析 (3)5
【解析】
试题分析:1)图(1)中与△ADE相似的有△ABD,△ACD,△DCE.
证明:∵AB=AC,D为BC的中点,
∴AD⊥BC,∠B=∠C,∠BAD=∠CAD,
又∵∠MDN=∠B,
∴△ADE∽△ABD,
同理可得:△ADE∽△ACD,
∵∠MDN=∠C=∠B,
∠B+∠BAD=90°,∠ADE+∠EDC=90°,
∠B=∠MDN,
∴∠BAD=∠EDC,
∵∠B=∠C,
∴△ABD∽△DCE,
∴△ADE∽△DCE,
(2)△BDF∽△CED∽△DEF,
证明:∵∠B+∠BDF+∠BFD=180°
∠EDF+∠BDF+∠CDE=180°,
又∵∠EDF=∠B,∴∠BFD=∠CDE,
由AB=AC,得∠B=∠C,
∴△BDF∽△CED,
∴![]() .
.
∵BD=CD,
∴![]() .
.
又∵∠C=∠EDF,
∴△BDF∽△CED∽△DEF.
(3)连接AD,过D点作DG⊥EF,DH⊥BF,垂足分别为G,H.
∵AB=AC,D是BC的中点,
∴AD⊥BC,BD=![]() BC=6.
BC=6.
在Rt△ABD中,AD2=AB2﹣BD2,
∴AD=8
∴S△ABC=![]() BCAD=
BCAD=![]() ×12×8=48.
×12×8=48.
S△DEF=![]() S△ABC=
S△ABC=![]() ×48=12.
×48=12.
又∵![]() ADBD=
ADBD=![]() AB.DH,
AB.DH,
∴DH=![]() =
=![]() =
=![]() ,
,
∵△BDF∽△DEF,
∴∠DFB=∠EFD
∵DG⊥EF,DH⊥BF,
∴DH=DG=![]() .
.
∵S△DEF=![]() ×EF×DG=12,
×EF×DG=12,
∴EF=![]() =5.
=5.