题目内容
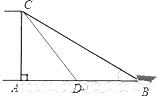
【题目】如图，有人在岸上点C的地方，用绳子拉船靠岸开始时，绳长CB=5米，拉动绳子将船身向岸边行驶了2米到点D后，绳长CD=
米，求岸上点C离水面的高度CA．
【答案】3米．
【解析】试题分析：
设AD= 
米，则由题意可知：AB=BD+AD=
米，∠CAB=90°，由此根据勾股定理可得：在Rt△ABC中，AC2=CB2-AB2，在Rt△ADC中，AC2=CD2-AD2，由此可得：CB2-AB2=CD2-AD2，即： 
，解方程求得
的值，将所求
的值代入：AC2=CD2-AD2即可求得AC的值.
试题解析：
由题意可知：∠CAB=90°，
∴在Rt△ABC中，AC2=CB2-AB2，在Rt△ADC中，AC2=CD2-AD2，
∴CB2-AB2=CD2-AD2.
设AD= 
米，则由题意可知：AB=BD+AD=
米，
∴
，解得： 
，即AD=2米.
∴AB=2+2=4（米），
∴AC2=CB2-AB2=25-16=9，
∴AC=3（米）.
答：点C离水面高度AC为3米．
练习册系列答案
相关题目
