题目内容
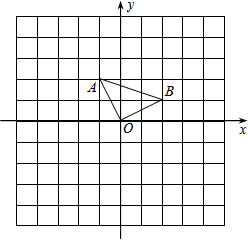
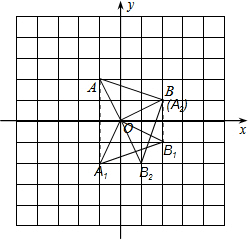
如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.
⑴ 画出△AOB关于x轴的对称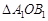 .
.
⑵ 画出将△AOB绕点O顺时针旋转90°的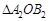 ,并判断
,并判断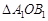 和
和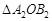 在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
⑶ 若将△AOB绕点O旋转360°,试求出线段AB扫过的面积.
⑴ 画出△AOB关于x轴的对称
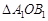 .
.⑵ 画出将△AOB绕点O顺时针旋转90°的
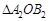 ,并判断
,并判断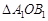 和
和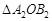 在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.⑶ 若将△AOB绕点O旋转360°,试求出线段AB扫过的面积.

⑴ 画图见解析;⑵画图见解析,轴对称,对称轴为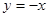 ;⑶
;⑶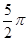 .
.
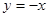 ;⑶
;⑶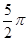 .
.试题分析:(1)根据轴对称的性质,找到A、B的对称点,顺次连接可得△A1OB1.
(2)根据旋转三要素找到A2、B2,顺次连接即可,结合图形可判断△A1OB1和△A2OB2是轴对称关系.(3)线段AB扫过的面积是圆环,过点O作OE⊥AB,以OA为半径的圆的面积减去以OE为半径的圆的面积,即可求出答案.
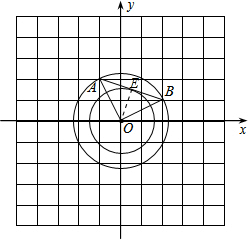
⑴ 画图如下:
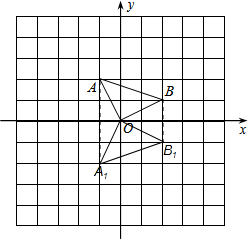
⑵ 画图如下:
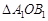 和
和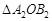 成轴对称,对称轴为
成轴对称,对称轴为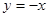 .
.⑶ 如图,过点O作OE⊥AB,线段AB扫过的面积=
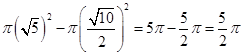 .
.

练习册系列答案
相关题目
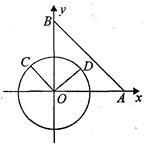
 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点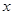 轴交于
轴交于 ,
,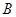 两点,
两点, 为弦,
为弦,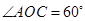 ,
,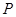 是
是 。
。 的度数为 ;
的度数为 ;  的长;
的长;  上时,
上时, ,问
,问 为何值时,
为何值时, 是等腰三角形?
是等腰三角形?
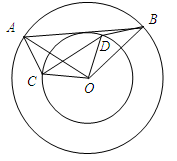
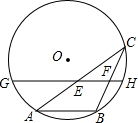
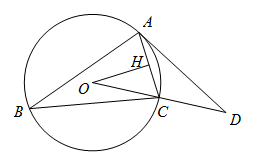
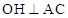 于H,
于H, ,过A点的直线与OC的延长线交于点D,
,过A点的直线与OC的延长线交于点D,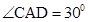 ,
,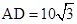 .
.
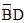 上一点,∠DAC=∠AED.
上一点,∠DAC=∠AED.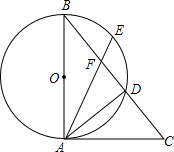
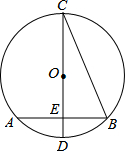
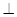 CD,垂足为E,连接BC,若AB=
CD,垂足为E,连接BC,若AB=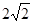 cm,
cm,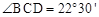 ,则圆O的半径为 cm.
,则圆O的半径为 cm.