Question

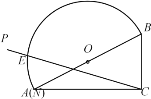
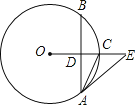
【题目】如图，在⊙O中，半径OC垂直于弦AB，垂足为点D，点E在OC的延长线上，∠EAC＝∠BAC

(1)求证：AE是⊙O的切线；

(2)若AB＝8，cosE＝，求CD的长．

Answer 1

【答案】（1）见解析；（2）CD= 2．

【解析】

（1）连接OA，求出∠AOC=∠BAE，求出∠OAE=90°，根据切线的判定得出即可；

（2）根据垂径定理求出AD，证明△ODA∽△OAE，得到∠OAD=∠E，根据正切的定义计算即可．

（1）证明：连接OA，

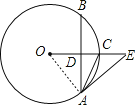
∵AB⊥OC，OC过O，
∴，
∴∠CAB=∠AOC，
∵∠EAC=∠BAC，
∴∠EAB=∠AOC，
∵OC⊥AB，
∴∠ODA=90°，
∴∠OAB+∠AOC=90°，
∴∠OAB+∠BAE=90°，
即OA⊥AE，
∵OA过点O，
∴AE是⊙O的切线；

（2）解：∵OD⊥AB，AB=8，

∴AD=AB=4，

∵∠OAE=∠ODA=90°，∠O=∠O，

∴△ODA∽△OAE，

∴∠OAD=∠E，

∵cosE=，

∴cos∠OAD=，

∴OA=5，

∴OD=3，

∴CD=OC-OD=5-3=2．