ЬтФПФкШн
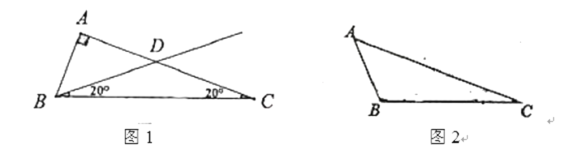
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФБпOAдкxжсе§АыжсЩЯЃЌБпOCдкyжсе§АыжсЩЯЃЌBЕуЕФзјБъЮЊ(1ЃЌ3)ЃЎОиаЮO'A'BC'ЪЧОиаЮOABCШЦBЕуФцЪБеыа§зЊЕУЕНЕФЃЎO'ЕуЧЁКУдкxжсЕФе§АыжсЩЯЃЌ O'C'НЛABгкЕуD.
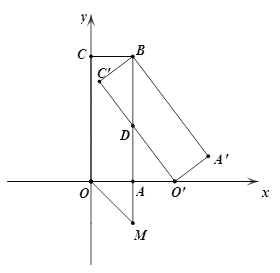
(1)ЧѓЕуO'ЕФзјБъЃЌВЂХаЖЯЁїO'DBЕФаЮзДЃЈвЊЫЕУїРэгЩЃЉ
(2)ЧѓБпC'O'ЫљдкжБЯпЕФНтЮіЪНЃЎ
(3)бгГЄBAЕНMЪЙAM=1ЃЌдк(2)жаЧѓЕУЕФжБЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУІЄPOMЪЧвдЯпЖЮOMЮЊжБНЧБпЕФжБНЧШ§НЧаЮ?ШєДцдкЃЌЧыжБНгаДГіPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)ЕуO'ЕФзјБъ(2ЃЌ0)ЃЌЁїO'DBЮЊЕШбќШ§НЧаЮЃЌРэгЩТдМћНтЮіЃЛ(2)БпC'O'ЫљдкжБЯпЕФНтЮіЪНЃК![]() ЃЛ (3)P(2,0)ЃЌ
ЃЛ (3)P(2,0)ЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгOBЃЌOЁфBЃЌИљОна§зЊЕФаджЪПЩЕУOB=OЁфBЃЌдйИљОнОиаЮЕФаджЪBAЁЭOAЃЌдйИљОнЕШбќШ§НЧаЮШ§ЯпКЯвЛЕФаджЪПЩЕУAO=AOЁфЃЌШЛКѓИљОнЕуBЕФзјБъЧѓГіAOЕФГЄЖШЃЌдйЕУЕНAOЁфЕФГЄЖШЃЌЕуOЁфЕФзјБъМДПЩЕУЕНЃЛРћгУНЧНЧБпжЄУїЁїBCЁфDгыЁїOЁфADШЋЕШЃЌШЛКѓИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНBD=OЁфDЃЌЫљвдЁїOЁфDBЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉЩшЕуDЕФзјБъЪЧЃЈ1ЃЌaЃЉЃЌБэЪОГіOЁфDЕФГЄЖШЃЌШЛКѓРћгУЙДЙЩЖЈРэСаЪНЧѓГіaЕФжЕЃЌДгЖјЕУЕНЕуDЕФзјБъЃЌдйИљОнД§ЖЈЯЕЪ§ЗЈСаЪНМДПЩЧѓГіжБЯпCЁфOЁфЕФНтЮіЪНЃЛ
ЃЈ3ЃЉИљОнAM=1ПЩЕУЁїAOMЪЧЕШбќжБНЧШ§НЧаЮЃЌШЛКѓЗжЂйPMЪЧСэвЛжБНЧБпЃЌЁЯPMA=45ЁуЃЌЂкPOЪЧСэвЛжБНЧБпЃЌЁЯPOA=45ЁуСНжжЧщПіСаЪННјааМЦЫуМДПЩЕУНтЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌСЌНгOBЃЌOЁфBЃЌдђOB=OЁфBЃЌ
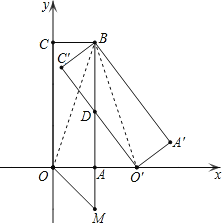
ЁпЫФБпаЮOABCЪЧОиаЮЃЌ
ЁрBAЁЭOAЃЌ
ЁрAO=AOЁфЃЌ
ЁпBЕуЕФзјБъЮЊЃЈ1ЃЌ3ЃЉЃЌ
ЁрOA=1ЃЌ
ЁрAOЁф=1ЃЌ
ЁрЕуOЁфЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌ
ЁїOЁфDBЮЊЕШбќШ§НЧаЮЃЌ
РэгЩШчЯТЃКдкЁїBCЁфDгыЁїOЁфADжаЃЌ
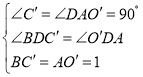
ЁрЁїBCЁфDЁеЁїOЁфADЃЈAASЃЉЃЌ
ЁрBD=OЁфDЃЌ
ЁрЁїOЁфDBЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉЩшЕуDЕФзјБъЮЊЃЈ1ЃЌaЃЉЃЌдђAD=aЃЌ
ЁпЕуBЕФзјБъЪЧЃЈ1ЃЌ3ЃЉЃЌ
ЁрOЁфD=3-aЃЌ
дкRtЁїADOЁфжаЃЌAD2+AOЁф2=OЁфD2ЃЌ
Ёрa2+12=ЃЈ3-aЃЉ2ЃЌ
НтЕУ![]()
ЁрЕуDЕФзјБъЮЊ![]()
ЩшжБЯпCЁфOЁфЕФНтЮіЪНЮЊy=kx+bЃЌ
дђ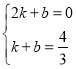 НтЕУ
НтЕУ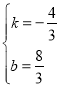
ЁрБпCЁфOЁфЫљдкжБЯпЕФНтЮіЪНЃК![]()
ЃЈ3ЃЉЁпAM=1ЃЌAO=1ЃЌЧвAMЁЭAOЃЌ
ЁрЁїAOMЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЂйPMЪЧСэвЛжБНЧБпЪБЃЌЁЯPMA=45ЁуЃЌ
ЁрPA=AM=1ЃЌЕуPгыЕуOЁфжиКЯЃЌ
ЁрЕуPЕФзјБъЪЧЃЈ2ЃЌ0ЃЉЃЌ
ЂкPOЪЧСэвЛжБНЧБпЃЌЁЯPOA=45ЁуЃЌдђPOЫљдкЕФжБЯпЮЊy=xЃЌ
Ёр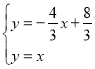
НтЕУ![]()
ЁрЕуPЕФзјБъЮЊPЃЈ2ЃЌ0ЃЉЛђ![]()

 МтзгЩњаТПЮЬУПЮЪБзївЕЯЕСаД№АИ
МтзгЩњаТПЮЬУПЮЪБзївЕЯЕСаД№АИ гЂВХМЦЛЎЭЌВНПЮЪБИпаЇбЕСЗЯЕСаД№АИ
гЂВХМЦЛЎЭЌВНПЮЪБИпаЇбЕСЗЯЕСаД№АИ