题目内容
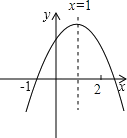
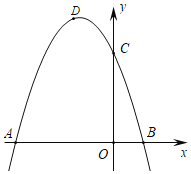
【题目】如图，抛物线C1的图象与x轴交A(﹣3，0)，B(1，0)两点，与y轴交于点C(0，3)点D为抛物线的顶点．
（1）求抛物线C1的解析式；
（2）将抛物线C1关于直线x＝1对称后的抛物线记为C2，将抛物线C1关于点B对称后的抛物线记为C3，点E为抛物线C3的顶点，在抛物线C2的对称轴上是否存在点F，使得△BEF为等腰三角形？若存在请求出点F的坐标，若不存在请说明理由．
【答案】（1）y＝﹣x2﹣2x+3；（2）存在，当点F为(3，﹣4+2
)或(3，﹣4﹣2)或(3，4)或(3，﹣
)时，使得△BEF为等腰三角形
【解析】
（1）将A、B、C三点代入一般式，即可求出解析式；
（2）由折叠的性质和旋转的性质可求抛物线C2解析式和抛物线C3解析式，可得点E坐标，由等腰三角形的性质可求点F坐标．
解：（1）设解析式y＝a（x﹣1）（x+3）
将C（0，3）代入得 a＝﹣1
∴抛物线C1的解析式为y＝﹣x2﹣2x+3；
（2）∵抛物线C1的解析式为y＝﹣x2﹣2x+3；
∴抛物线C1的顶点为（﹣1，4）
∵将抛物线C1关于直线x＝1对称后的抛物线记为C2，将抛物线C1关于点B对称后的抛物线记为C3，
∴抛物线C2解析式为：y＝﹣（x﹣3）2+4，抛物线C3解析式为：y＝（x﹣3）2﹣4，
∵点E为抛物线C3的顶点，
∴点E（3，﹣4），
∴BE=
，
∵点F抛物线C2的对称轴上，
∴点F横坐标为3，
若BE＝EF＝2，则点F坐标为（3，﹣4+2）或（3，﹣4﹣2），
若BE＝BF时，则点F与点E关于x轴对称，
∴点F（3，4），
若BF＝EF时，则22+（4﹣EF）2＝BF2，
∴BF＝EF＝
，
∴点F（3，﹣），
综上所述：当点F为（3，﹣4+2）或（3，﹣4﹣2）或（3，4）或（3，﹣）时，使得△BEF为等腰三角形
