题目内容
【题目】如图,ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
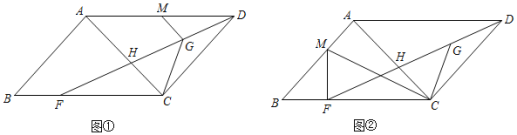
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2![]() ,求GM;
,求GM;
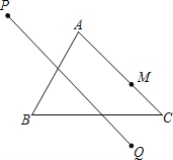
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先根据平行四边形的性质和平行线的性质得出∠BAC=∠ACD=90,进而得出HD=![]() ,然后根据角平分线的性质和等腰三角形的性质得出CD=CF=8,然后由勾股定理求出CH的长度,从而求出AH的长度,最后利用三角形中位线的性质即可得出MG的长度;
,然后根据角平分线的性质和等腰三角形的性质得出CD=CF=8,然后由勾股定理求出CH的长度,从而求出AH的长度,最后利用三角形中位线的性质即可得出MG的长度;
(2)过点D作DN∥AC,交CG的延长线于点N,首先利用AAS证明△CGH≌△NGD得出GC=GN,从而有CN=2CG,然后通过平行四边形的性质和平行线的性质得出∠MFC=∠NDC,∠FCM=∠DCN,再加上CF=CD利用ASA即可证△MFC≌△NDC,从而得出CM=CN,即可证明CM=2CG.
(1)∵四边形ABCD是平行四边形,
![]() ,
,
∵AB⊥AC,
∴∠BAC=∠ACD=90°,
∵G为DH的中点,
∴CG=HG=GD,
∵CG=![]() ,
,
∴HD=![]() ,
,
∵DF平分∠ADC,
∴∠DFC=∠ADF=∠CDF,
∴CF=CD,
∵CF=8,
∴CD=8,
在Rt△HCD中,HC=![]() ,
,
∵AC=9,
∴AH=5,
∵M为AD的中点,G为DH的中点,
∴MG=![]() AH=
AH=![]() ;
;
(2)如图②,过点D作DN∥AC,交CG的延长线于点N,
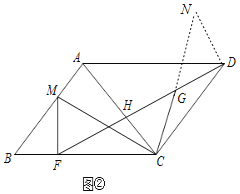
∵DN∥AC,
∴∠N=∠ACN,∠DAC=∠ADN,
∵G为DH的中点,
∴DG=HG,且∠N=∠ACG,∠CGH=∠DGN,
∴△CGH≌△NGD(AAS)
∴GC=GN,
∴CN=2CG,
∵∠MCD=∠BCG,
∴∠FCM=∠DCN,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠DAC=∠ACB=∠ADN,
∵∠MFB=∠BAC,∠B=∠B,且∠BMF=180°﹣∠B﹣∠BFM,∠ACB=180°﹣∠B﹣∠BAC,
∴∠BMF=∠ACB,
∴∠BMF=∠ADN,
∴∠BMF+∠B=∠ADN+∠ADC,
∴∠MFC=∠NDC,且CF=CD,∠FCM=∠DCN,
∴△MFC≌△NDC(ASA)
∴CM=CN,
∴CM=2CG.