题目内容
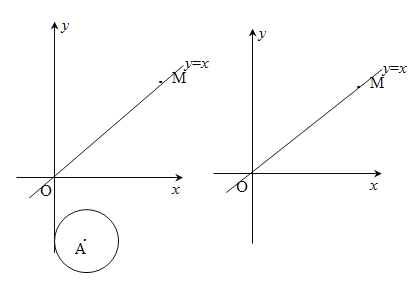
【题目】如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.
(1)填空:
①直线OM与x轴所夹的锐角度数为 °;
②当t= 时,⊙A与坐标轴有两个公共点;
(2)求出运动过程中⊙A与直线OM相切时的t的值.
【答案】(1)①45;②1秒或2秒或3秒;(2)![]() 或
或![]() .
.
【解析】
(1)①利用直线y=x上点的坐标特征易得直线y=x为第一、三象限的角平分线,则直线OM与x轴所夹的锐角度数为45°;
②根据直线与圆的位置关系得到⊙A沿y轴正方向运动时,⊙A始终与y轴相切,所以当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点,易得t=1或t=2或t=3;
(2)分两种情况画出图形,解答即可.
(1)①∵直线y=x上点到x轴和y轴的距离相等,∴直线y=x为第一、三象限的角平分线,∴直线OM与x轴所夹的锐角度数为45°;
②∵⊙A的半径为1,圆心A点的坐标为(1,﹣2),∴⊙A沿y轴正方向运动时,⊙A始终与y轴相切,当⊙A与x轴相切或点A在x轴上时,⊙A与坐标轴有两个公共点.
当⊙A与x轴相切时,则点A与x轴的距离为1,得到t=1或3;
当点A在x轴上,则t=2;
所以t=1或t=2或t=3.
故答案为:45,1秒或2秒或3秒;
(2)分两种情况讨论:
①如图1,作AB⊥y轴于B,AC⊥直线OM于C,AH⊥x轴于H,交直线OM于P,则OB=t﹣2,AB=AC=1,OH=1.
∵直线OM与x轴所夹的锐角度数为45°,∴∠POH=45°,∴∠OPH=45°,∴∠APC=45°,∴△OPH和△APC都是等腰直角三角形,∴PH=OH=1,AP![]() AC
AC![]() ,∴AH=AP+PH
,∴AH=AP+PH![]() 1,而AH=OB,∴t﹣2
1,而AH=OB,∴t﹣2![]() ,∴t=
,∴t=![]() ;
;
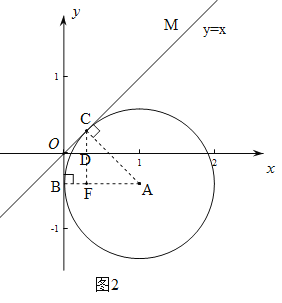
②如图2,作AB⊥y轴于B,AC⊥直线OM于C,CD⊥x轴于D,CD交BA与F,则OB=DF=2﹣t,AB=AC=1.
∵OB、OC都是⊙A的切线,∴OB=OC=2﹣t.
∵直线OM与x轴所夹的锐角度数为45°,∴∠COD=45°,∴△ODC是等腰直角三角形,∠OCD=45°,∴OD=CD=![]() =
=![]() .
.
∵∠OCA=90°,∠OCD=45°,∴∠ACF=45°,∴△ACF是等腰直角三角形,∴AC![]() AF.
AF.
∵AF=BA-BF=![]() ,∴
,∴![]() =1,解得:∴2﹣t=
=1,解得:∴2﹣t=![]() ,∴t=
,∴t=![]() .
.
综上所述:![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案