ЬтФПФкШн
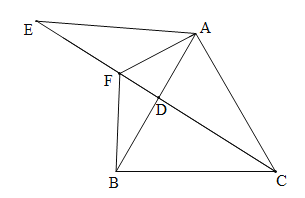
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ0ЃЌaЃЉЃЌBЃЈbЃЌ0ЃЉЧвaЁЂbТњзу|a+2bЉ6|+|aЉ2b+2|ЃН0ЃЎEЮЊЯпЖЮABЩЯвЛЖЏЕуЃЌЁЯBEDЃН![]() ЁЯOABЃЌBDЁЭECЃЌДЙзудкECЕФбгГЄЯпЩЯЃЌЪдЧѓЃК
ЁЯOABЃЌBDЁЭECЃЌДЙзудкECЕФбгГЄЯпЩЯЃЌЪдЧѓЃК

ЃЈ1ЃЉХаЖЯЁїOABЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
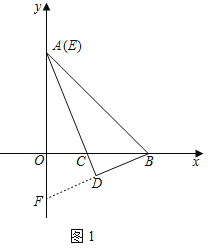
ЃЈ2ЃЉШчЭМ1ЃЌЕБЕуEгыЕуAжиКЯЪБЃЌЬНОПЯпЖЮACгыBDЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуEдкЯпЖЮABЃЈВЛгыAЁЂBжиКЯЃЉЩЯдЫЖЏЪБЃЌЪдЬНОПЯпЖЮECгыBDЕФЪ§СПЙиЯЕЃЌжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЛЃЈ2ЃЉACЃН2BDЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉECЃН2BDЃЌжЄУїМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЗЧИКадЕУГіaЃЌbЕФжЕНјЖјНтД№МДПЩЃЎ
ЃЈ2ЃЉбгГЄBDгыyжсНЛгкЕуFЃЌжЄУїЁїABDЁеЁїAFDЃЌПЩЕУBDЃНDFЃЌдйжЄУїЁїAOCЁеЁїBOFЃЌПЩЕУACЃНBFЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЙ§ЕуEзїENЁЭxжсгкЕуKЃЌНЛBDЕФбгГЄЯпгкЕуNЃЌжЄУїЁїEBDЁеЁїENDЃЌПЩЕУBDЃНDNЃЌдйжЄУїЁїEKCЁеЁїBKNЃЌПЩЕУECЃНBNЃЌдђНсТлЕУжЄЃЎ
НтЃКЃЈ1ЃЉЁп|a+2bЉ6|+|aЉ2b+2|ЃН0ЃЌ|a+2bЉ6|Ён0ЃЌ|aЉ2b+2|Ён0
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрOAЃНOBЃЌ
гжЁпЁЯAOBЃН90ЁуЃЌ
ЁрЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ2ЃЉACЃН2BDЃЌРэгЩШчЯТЃКШчЭМ1ЃЌбгГЄBDгыyжсНЛгкЕуFЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрЁЯBADЃНЁЯFAD
гжЁпBDЁЭECЃЌЁЯADBЃНЁЯADFЃЌ
дкЁїADBКЭЁїADFжаЃЌ
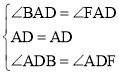 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїAFDЃЈASAЃЉЃЌ
ЁрBDЃНDFЃЌ
Ёп![]()
Ёр![]()
дкЁїAOCКЭЁїBOFжа
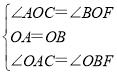
ЁрЁїAOCЁеЁїBOFЃЈASAЃЉЃЌ
ЁрACЃНBFЃЌ
ЁрACЃН2BDЃЛ
ЃЈ3ЃЉECЃН2BDЃЌжЄУїШчЯТЃК
ШчЭМ2ЃЌЙ§ЕуEзїENЁЭxжсгкЕуKЃЌНЛBDЕФбгГЄЯпгкЕуNЃЌ
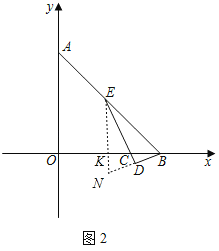
ЁрENЁЮyЃЌ
ЁрЁЯNEBЃНЁЯOABЃЌ
ЁпЁЯBEDЃН![]() ЁЯOABЃЌ
ЁЯOABЃЌ
ЁрЁЯNEDЃНЁЯBEDЃЌ
дкЁїEBDКЭЁїENDжаЃЌ
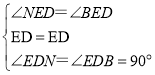 ЃЌ
ЃЌ
ЁрЁїEBDЁеЁїENDЃЈASAЃЉЃЌ
ЁрBDЃНDNЃЌ
![]()
Ёр![]()
дкЁїEKCКЭЁїBKNжаЃЌ
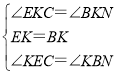
ЁрЁїEKCЁеЁїBKNЃЈASAЃЉЃЌ
ЁрECЃНBNЃЌ
ЁрECЃН2BDЃЎ