Question

【题目】如图，在等边三角形ABC中，点D在线段AB上，点E在CD的延长线上，连接AE，AE=AC，AF平分∠EAB，交CE于点F，连接BF.

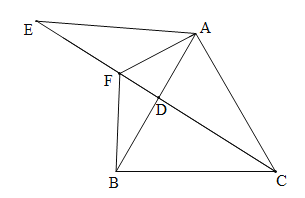
（1）求证：EF=BF；

（2）猜想∠AFC的度数，并说明理由.

Answer 1

【答案】（1）证明见解析；（2）∠AFC=60°，理由见解析.

【解析】

（1）根据SAS证明△AEF≌△ABF，根据全等三角形对应边相等即可得出结论；

（2）根据全等三角形对应角相等，得到∠E=∠FBA，∠EFA=∠BFA.根据等边对等角得到∠E=∠ACE，等量代换得到∠FBA=∠ACE，根据三角形内角和为180°得到∠BFD=∠BAC=60°.根据60°+∠DFA=180°－∠DFA变形即可得到结论.

（1）∵△ABC是等边三角形，

∴AB=AC，∠BAC=60°.

∵AE=AC，

∴AE=AB.

∵AF平分∠EAB，

∴∠EAF=∠BAF.

∵AE=AB，∠EAF=∠BAF，AF=AF，

∴△AEF≌△ABF(SAS)，

∴EF=BF.

（2）∠AFC=60°.理由如下：

∵△AEF≌△ABF，

∴∠E=∠FBA，∠EFA=∠BFA.

∵AE=AC，

∴∠E=∠ACE，

∴∠FBA=∠ACE.

∵∠FDB=∠ADC，

∴∠BFD=∠BAC=60°.

∵∠EFA=180°－∠DFA，

∴60°+∠DFA=180°－∠DFA，

∴∠DFA=60°，

即∠AFC=60°.