Question

【题目】如图，直线y＝x＋8与x轴，y轴分别交于点A，B，直线y＝x＋1与直线AB交于点C，与y轴交于点D．

（1）求点C的坐标．

（2）求△BDC的面积．

（3）如图，P是y轴正半轴上的一点，Q是直线AB上的一点，连接PQ．

①若PQ∥x轴，且点A关于直线PQ的对称点A′恰好落在直线CD上，求PQ的长．

②若△BDC与△BPQ全等(点Q不与点C重合)，请写出所有满足要求的点Q坐标(直接写出答案).

Answer 1

【答案】（1）C(3,4)；（2）；（3）①；②Q(，)

【解析】

（1）联立方程解答即可得出点C的坐标；

（2）根据三角形的面积公式解答即可；

（3）①根据PQ∥x轴得出AA'⊥x轴，进而解答即可；

②分两种情况进行解答即可．

（1）由x＋8=x+1得x=3,代入得y=3+1=4,

∴ C(3,4)

（2）∵ B(0,8), D(0,1),

∴ BD=7. C(3,4)

∴S△BDCBD×3×7×3=

（3）①∵ PQ//x轴,∴AA′⊥轴.

∵ A(6,0), ∴ AA'=6+1=7

∴ y=x＋8

∴ x=，即：PQ

②按2种情形讨论

若P在点B下方，则有BP＝BC＝5，

此时xQ＝＝

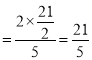
代入y＝x＋8得yQ，

∴ Q( ，)．

P在点B上方时，

若BP=BD，

则有xQ=-xC=-3

∴ Q(-3，12)，

若BP＝BC＝5，

则有xQ3＝－xQ1＝－，

<>∴Q(，)．