Question

【题目】已知：如图，在直角三角形ABC中，∠BAC=90°，AB=AC，D为BC的中点，E为AC上一点，点G在BE上，连接DG并延长交AE于F，若∠FGE=45°．

（1）求证：BDBC=BGBE；

（2）求证：AG⊥BE；

（3）若E为AC的中点，求EF：FD的值．

Answer 1

【答案】（1）（2）见解析（3）

【解析】

试题（1）根据题意，易证△GBD∽△CBE，得，即BDBC=BGBE；

（2）可通过证明ABG∽△EBA从而求得AG⊥BE；

（3）首先连接DE，E是AC中点，D是BC中点，得出DE∥BA，因为BA⊥AC，所以 DE⊥AC设AB=2a AE=a，做CH⊥BE交BE的延长线于H，再利用△AEG≌△CEH，以及△DEF∽△BHC得出即可．

试题解析：（1）证明：∵∠BAC=90°，AB=AC，∴∠ABC=∠C=45°．∵∠BGD=∠FGE=45°，∴∠C=∠BGD．∵∠GBC=∠GBC，∴△GBD∽△CBE，∴，即BDBC=BGBE；

（2）证明：∵BDBC=BGBE，∠C=45°，∴BG====，∴=，∠ABG=∠EBA，∴△ABG∽△EBA，∴∠BGA=∠BAE=90°，∴AG⊥BE；

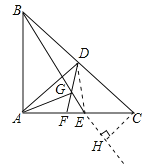
（3）解：连接DE，连接DE，E是AC中点，D是BC中点，∴DE∥BA．∵BA⊥AC，∴DE⊥AC，设AB=2a AE=a，做CH⊥BE交BE的延长线于H．∵∠AEG=∠CEH，∠AGE=∠CHE，AE=EC，∴△AEG≌△CEH（AAS），∴CH=AG，∠GAE=∠HCE．∵∠BAE为直角，∴BE=a，∴AG=AB×=a=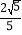a，∴CH=a．∵AG⊥BE，∠FGE=45°，∴∠AGF=45°=∠ECB．∵∠FGE=45°，∴∠AGE=90°，∴AG∥CH，∴∠GAE=∠HCE．∵∠DFE=∠GAE+∠AGF=∠HCE+∠ECB，∴∠DFE=∠BCH．又∵DE⊥AC，CH⊥BE，∴△DEF∽△BHC，∴EF：DF=CH：BC=a：2a=．