题目内容
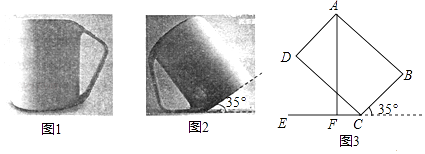
【题目】已知:点C在∠AOB的一边OA上,过点C的直线DE∥O B.做∠ACD的平分线CF,过点C画CF的垂线CG,如图所示.
(Ⅰ)若∠AOB=40°,求∠ACD及∠ECF的度数;
(Ⅱ)求证:CG平分∠OCD;
(Ⅲ)延长FC交OB于点H,用直尺和三角板过点O作OR⊥FH,垂足为R,过点O
作FH的平行线交ED于点Q.先补全图形,再证明∠COR=∠GCO,∠CQO=∠CHO.

【答案】(1)110°;(2)详见解析;(3)详见解析.
【解析】
(Ⅰ)根据平行线的性质和角平分线的性质,可以求得∠ECF的度数;
(Ⅱ)根据角平分线的性质、平角的定义可以求得∠OCG和∠DCG的关系,从而可以证明结论成立.
(Ⅲ)画出图形,只要证明CG∥OR,四边形OHCQ是平行四边形即可解决问题;
(Ⅰ)解:∵直线DE∥OB,CF平分∠ACD,∠O=40°,
∴∠ACE=∠O,∠ACF=∠FCD,
∴∠ACE=40°,
∴∠ACD=140°,
∴∠ACF=70°,
∴∠ECF=∠ECA+∠ACF=40°+70°=110°;
(Ⅱ)证明:∵CF平分∠ACD,CG⊥CF,∠ACD+∠OCD=180°,
∴∠ACF=∠FCD,∠FCG=90°,
∴∠FCD+∠DCG=90°,∠ACF+∠OCG=90°,
∴∠DCG=∠OCG,
∴CG平分∠OCD.
(Ⅲ)解:图形如图所示,
理由:∵GC⊥FH,OR⊥FH,
∴GC∥OR,
∴∠COR=∠GCO.
∵CQ∥OH,OQ∥CH,
∴四边形OHCQ是平行四边形,
∴∠CQO=∠OHC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目