题目内容
【题目】在劳技课上,老师请同学们在一张长为17cm,宽为16 cm的长方形纸板上剪下一个腰长为10cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).请你帮助同学们设计出不同类型的,你认为符合条件的等腰三角形,(分别在下列矩形中画出示意图)并分别计算剪下的等腰三角形的面积.(位置不同,形状全等的将视为一种结果)
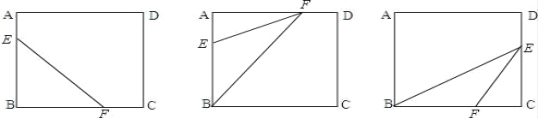
【答案】画图参见解析,50cm2;40cm2;5![]() cm2.
cm2.
【解析】
试题分析:(1)在BA、BC上分别截取BE=BF=10cm;(2)在BA上截取BE=10,以E为圆心,10长为半径作弧,交AD于F;(3)在BC上截取BF=10,以F为圆心10为半径作弧,交CD于E.
试题解析:如图所示:
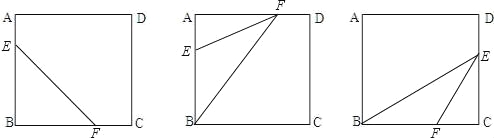
(1)以B为等腰三角形的一个顶点,在BA、BC上分别截取BE=BF=10cm,则等腰三角形的面积是10×10÷2=50cm2;(2)B点作为等腰三角形的一个顶点,在BA上截取BE=10,以E为圆心,10长为半径作弧,交AD于F;AE=16﹣10=6cm,AF=![]() =8cm,则此等腰三角形的面积是10×8÷2=40cm2;(3)B点作为等腰三角形的一个顶点,在BC上截取BF=10,以F为圆心,10为半径作弧,交CD于E.CF=17﹣10=7cm,
=8cm,则此等腰三角形的面积是10×8÷2=40cm2;(3)B点作为等腰三角形的一个顶点,在BC上截取BF=10,以F为圆心,10为半径作弧,交CD于E.CF=17﹣10=7cm,
EC=![]() =
=![]() cm,则此等腰三角形的面积是10×
cm,则此等腰三角形的面积是10×![]() ÷2=5
÷2=5![]() cm2.
cm2.

练习册系列答案
相关题目
