题目内容
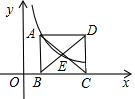 如图,已知点(1,3)在函数y=
如图,已知点(1,3)在函数y=| k |
| x |
| k |
| x |
分析:把已知点的坐标代入函数解析式即可求出k的值,把k的值代入得到函数的解析式,然后根据正方形的性质设出A和E的坐标,因为函数图象过这两点,把设出的两点坐标代入到函数解析式中得到①和②,联立即可求出a和b的值,得到E的坐标.
解答:解:把(1,3)代入到y=
得:k=3,
故函数解析式为y=
,
设A(a,
)(a>0),根据图象和题意可知,点E(a+
,
),
因为y=
的图象经过E,
所以将E代入到函数解析式中得:
(a+
)=3,
即a2=
,
求得:a=
或a=-
(不合题意,舍去),
∴a=
,
∴a+
=
,
则点E的横坐标为
.
故答案为:
.
| k |
| x |
故函数解析式为y=
| 3 |
| x |
设A(a,
| 3 |
| a |
| 3 |
| 2a |
| 3 |
| 2a |
因为y=
| 3 |
| x |
所以将E代入到函数解析式中得:
| 3 |
| 2a |
| 3 |
| 2a |
即a2=
| 3 |
| 2 |
求得:a=
| ||
| 2 |
| ||
| 2 |
∴a=
| ||
| 2 |
∴a+
| 3 |
| 2a |
| 6 |
则点E的横坐标为
| 6 |
故答案为:
| 6 |
点评:此题考查学生会根据一点的坐标求反比例的解析式,灵活运用正方形及反比例函数的性质解决实际问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )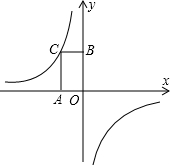 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=