Question

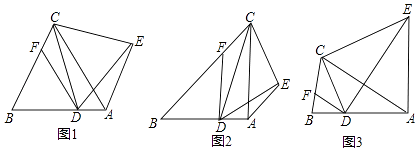
【题目】如图1，共顶点的两个三角形△ABC，△AB′C′，若 AB=AB′，AC=AC′，且∠BAC+∠B′AC′=180°，我们称△ABC 与△AB′C′互为“顶补三角形”．

(1)已知△ABC 与△ADE 互为“顶补三角形”，AF 是△ABC 的中线．

①如图 2，若△ADE 为等边三角形时，求证：DE=2AF；

②如图 3，若△ADE 为任意三角形时，上述结论是否仍然成立？请说明理由．

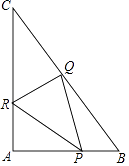
(2)如图4，四边形 ABCD 中，∠B+∠C=90°．在平面内是否存在点 P，使△PAD 与△PBC 互为“顶补三角形”， 若存在，请画出图形，并证明；若不存在，请说明理由．

Answer 1

【答案】(1) ①见解析 ②成立，理由见解析（2）存在点P，证明见解析.

【解析】

(1)①首先证明，再利用与互为“顶补三角形”，求得，，再利用是的中线和，即可证得；

②首先证明，然后根据，证得，再根据全等三角形对应边相等即可解决问题；

(2)先做辅助线，的垂直平分线，则的交点，然后利用垂直平分线定理，即可解决问题．

证明：（1）①如图25－1，

为等边三角形，

，

与互为“顶补三角形”，

，

是的中线，

，

，

，

即；

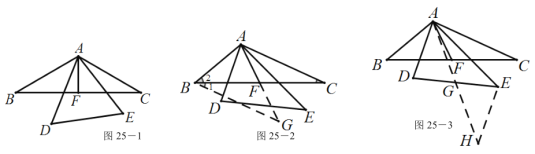
②方法一：如图25－2，

延长到，使，连接，

是的中线，

，又，

，

，，

，

又，，

，

即；方法二：如图25－3，

取中点，连接，并延长到，使，连接可证得， ，（方法同上）

又由是的中线，是的中线，

；

（2）存在点.如图25－4，分别作线段，的垂直平分线，则的交点，使得与互为“顶补三角形”.

证明：延长，交于点.

，

，

垂直平分于点，垂直平分于点，

，，， ，， ，

，

综上所述，与互为“顶补三角形”.