题目内容
【题目】如图,直角△ABC中,∠A为直角,AB=6,AC=8.点P,Q,R分别在AB,BC,CA边上同时开始作匀速运动,2秒后三个点同时停止运动,点P由点A出发以每秒3个单位的速度向点B运动,点Q由点B出发以每秒5个单位的速度向点C运动,点R由点C出发以每秒4个单位的速度向点A运动,在运动过程中: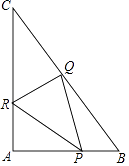
(1)求证:△APR,△BPQ,△CQR的面积相等;
(2)求△PQR面积的最小值;
(3)用t(秒)(0≤t≤2)表示运动时间,是否存在t,使∠PQR=90°?若存在,请直接写出t的值;若不存在,请说明理由.
【答案】
(1)解:如图,在Rt△ABC中,AB=6,AC=8,根据勾股定理得,BC=10,tan∠B= ![]() =
= ![]() =
= ![]()
![]() ,
,
过点Q作QE⊥AB于E,
在Rt△BQE中,BQ=5t,
∴sin∠B= ![]() =
= ![]() ,
,
∴QE=4t,
过点Q作QD⊥AC于D,
在Rt△CDQ中,CQ=BC﹣BQ=10﹣5t,
∴QD=CQsin∠C= ![]() (10﹣5t)=3(2﹣t),
(10﹣5t)=3(2﹣t),
由运动知,AP=3t,CR=4t,
∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),
∴S△APR= ![]() APAR=
APAR= ![]() ×3t×4(2﹣t)=6t(2﹣t),
×3t×4(2﹣t)=6t(2﹣t),
S△BPQ= ![]() BPQE=
BPQE= ![]() ×3(2﹣t)×4t=6t(2﹣t),
×3(2﹣t)×4t=6t(2﹣t),
S△CQR= ![]() CRQD=
CRQD= ![]() ×4t×3(2﹣t)=6t(2﹣t),
×4t×3(2﹣t)=6t(2﹣t),
∴S△APR=S△BPQ=S△CQR,
∴△APR,△BPQ,△CQR的面积相等;
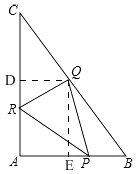
(2)解:由(1)知,S△APR=S△BPQ=S△CQR=6t(2﹣t),
∵AB=6,AC=8,
∴S△PQR=S△ABC﹣(S△APR+S△BPQ+S△CQR)
= ![]() ×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,
×6×8﹣3×6t(2﹣t)=24﹣18(2t﹣t2)=18(t﹣1)2+6,
∵0≤t≤2,
∴当t=1时,S△PQR最小=6;
(3)解:存在,由点P,Q,R的运动速度知,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,此时,四边形APQR是矩形,即:t=1秒时,∠PQR=90°,
由(1)知,QE=4t,QD=3(2﹣t),AP=3t,CR=4t,AR=4(2﹣t),
∴BP=AB﹣AP=6﹣3t=3(2﹣t),AR=AC﹣CR=8﹣4t=4(2﹣t),
过点Q作QD⊥AC于D,作QE⊥AB于E,∵∠A=90°,
∴四边形APQD是矩形,
∴AE=DQ=3(2﹣t),AD=QE=4t,
∴DR=|AD﹣AR|=|4t﹣4(2﹣t)|=4|2t﹣2|,PE=|AP﹣AE|=|3t﹣3(2﹣t)|=3|2t﹣2|
∵∠DQE=90°,∠PQR=90°,
∴∠DQR=∠EQP,
∴tan∠DQR=tan∠EQP,
在Rt△DQR中,tan∠DQR= ![]() =
= ![]() ,
,
在Rt△EQP中,tan∠EQP= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴16t=9(2﹣t),
∴t= ![]() .
.
即:t=1或 ![]() 秒时,∠PQR=90°.
秒时,∠PQR=90°.
【解析】(1)由面积公式可知求三角形的面积,缺高时,须作垂线补出高,用t的代数式表示△APR,△BPQ,△CQR的面积,在由斜边表示直角边时选用正弦;(2)用△ABC面积减去第(1)问中表示的△APR的面积的3倍,构建二次函数,在0≤t≤2范围内由二次函数的性质可求最值;(3)由点P,Q,R的运动速度知,3![]() 6=
6=![]() ,5
,5![]() 10=
10=![]() ,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,可证得四边形APQD是矩形,∠PQR=90°;若∠PQR=90
,运动1秒时,点P,Q,R分别在AB,BC,AC的中点,可证得四边形APQD是矩形,∠PQR=90°;若∠PQR=90![]() ,则∠DQR=∠EQP,用t的代数式表示两个角的正切,建立方程,求出t.
,则∠DQR=∠EQP,用t的代数式表示两个角的正切,建立方程,求出t.
【考点精析】通过灵活运用二次函数的最值和锐角三角函数的定义,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数即可以解答此题.

 口算题天天练系列答案
口算题天天练系列答案