题目内容
【题目】在数学活动课上，研究用正多边形镶嵌平面．请解决以下问题：
(1)用一种正多边形镶嵌平面
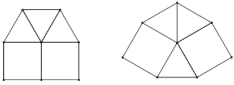
例如，用 6 个全等的正三角形镶嵌平面，摆放方案如图所示：
若用 m 个全等的正 n 边形镶嵌平面，求出 m，n 应满足的关系式；
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形，请画出两种不同的摆放方案；
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有 n 个，设这 n 个正多边形的边数分别为 x1，x2，…，xn，求出 x1，x2，…，xn 应满足的关系式．(用含 n 的式子表示)
【答案】（1）2m+2n=mn （2）见解析 （3）
+
+…+
=
【解析】
利用m、n表示多边形内角和即可得；
根据题意画出图形即可；
若镶嵌时每个顶点处的正多边形有 n 个，则把每个正多边形的内角加一起是360°，列出式子进行变形.
解：（1）正
边形的内角和为
，
故每个内角的度数为
，
依题意得：
，
整理得：
，
即
；
（2）如图：
（3）若镶嵌时每个顶点处的正多边形有 n 个，则
＝360°
180°n－
＝360°
＋…＋
.
练习册系列答案
相关题目
