题目内容
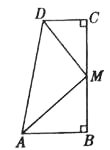
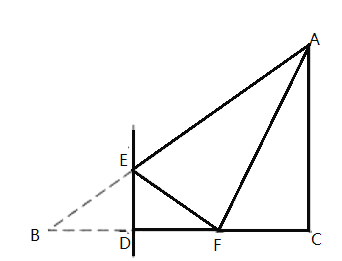
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,当
处,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的长.
的长.
【答案】1或2
【解析】
由题意根据翻折的性质以及勾股定理和特殊锐角三角函数值进行综合分析求解.
解:∵Rt△ABC中,∠ACB=90°,∠B=30°,
∴![]() ,
,
∵∠B=30°,DE⊥BC,
∴∠BED=60°,
由翻折的性质可知:∠BED=∠FED=60°,
∴∠AEF=60°,
∵△AEF为直角三角形,
∴∠EAF=30°,
∴AE=2EF,
由翻折的性质可知:BE=EF,
∴AB=3BE,
∴![]() ,
,
当点F在BC的延长线上时.
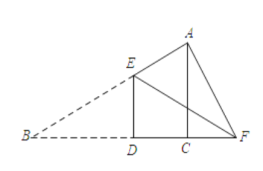
∵△AEF为直角三角形,
∴∠EAF=90°,
∴∠EFA=30°,
∴∠EFD=∠EFA,
又∵ED⊥BF,EA⊥AF,
∴AE=DE,
∵BC=3,∠ACB=90°,∠B=30°,
∴![]() ,
,
设![]() ,
,
∵DE∥AC,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴BD的长为1或2时,△AEF为直角三角形.

练习册系列答案
相关题目