Question

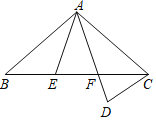
【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交AC边于点D，过点C作CF∥AB，与过点B的切线交于点F，连接BD.

(1)求证：BD＝BF；

(2)若AB＝10，CD＝4，求BC的长．

Answer 1

【答案】（1）详见解析；（2）BC的长为4.

【解析】试题分析：（1）根据圆周角定理求出BD⊥AC，∠BDC=90°，根据切线的性质得出AB⊥BF，求出∠ACB=∠FCB，根据角平分线性质得出即可；

（2）求出AC=10，AD=6，根据勾股定理求出BD，再根据勾股定理求出BC即可．

试题解析：（1）证明：∵AB＝AC，

∴∠ABC＝∠ACB.

∵CF∥AB，∴∠ABC＝∠FCB.

∴∠ACB＝∠FCB，

即CB平分∠DCF.

∵AB是⊙O的直径，∴∠ADB＝90°，即BD⊥AC.

∵BF是⊙的切线，∴BF⊥AB.

∵CF∥AB，∴BF⊥CF.

∴BD＝BF.

（2）∵AC＝AB＝10，CD＝4，

∴AD＝AC－CD＝10－4＝6.

在Rt△ABD中，BD2＝AB2－AD2＝102－62＝64.

在Rt△BDC中，BC＝＝＝4 .

即BC的长为4.