Question

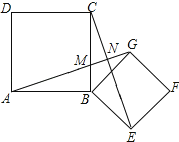
【题目】如图，四边形ABCD、为正方形，连接AG、CE.

（1）
求证：AG=CE；
（2）求证：AG⊥CE．

Answer 1

【答案】
（1）

证明：∵四边形ABCD、BEFG均为正方形，

∴AB=CB，∠ABC=∠GBE=90°，BG=BE，

∴∠ABG=∠CBE，

在△ABG和△CBE中，

，

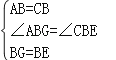∴△ABG≌△CBE（SAS），

∴AG=CE；

（2）

证明：如图所示：∵△ABG≌△CBE，

∴∠BAG=∠BCE，

∵∠ABC=90°，

∴∠BAG+∠AMB=90°，

∵∠AMB=∠CMN，

∴∠BCE+∠CMN=90°，

∴∠CNM=90°，

∴AG⊥CE．

【解析】（1）由正方形的性质得出AB=CB，∠ABC=∠GBE=90°，BG=BE，得出∠ABG=∠CBE，由SAS证明△ABG≌△CBE，得出对应边相等即可；
（2）由△ABG≌△CBE，得出对应角相等∠BAG=∠BCE，由∠BAG+∠AMB=90°，对顶角∠AMB=∠CMN，得出∠BCE+∠CMN=90°，证出∠CNM=90°即可．
此题根据全等三角形的判定和正方形的相关性质即可解答。