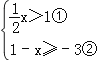Question

【题目】如图，在边长为6的正方形ABCD中，E是AB的中点，以E为圆心，ED为半径作半圆，交A、B所在的直线于M、N两点，分别以直径MD、ND为直径作半圆，则阴影部分面积为（　　）

A.9
B.18
C.36
D.72

Answer 1

【答案】B
【解析】解：根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积﹣大半圆的面积．
∵MN的半圆的直径，
∴∠MDN=90°．
在Rt△MDN中，MN2=MD2+DN2 ，
∴两个小半圆的面积=大半圆的面积．
∴阴影部分的面积=△DMN的面积．
在Rt△AED中，ED=
∴阴影部分的面积=△DMN的面积=．
故选：B．
【考点精析】本题主要考查了勾股定理的概念和扇形面积计算公式的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．