Question

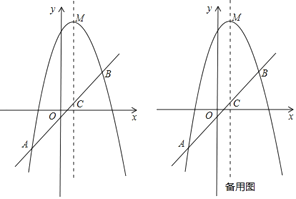
【题目】如图，⊙O的直径AB＝12，半径OC⊥AB，D为弧BC上一动点（不包括B、C两点），DE⊥OC，DF⊥AB，垂足分别为E．F．

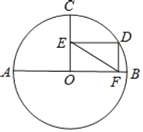
（1）求EF的长．

（2）若点E为OC的中点，

①求弧CD的度数．

②若点P为直径AB上一动点，直接写出PC+PD的最小值．

Answer 1

【答案】（1）EF＝6；（2）①弧CD的度数为60°；②PC+PD的最小值为6．

【解析】

(1)求出圆的半径，再判断出四边形OFDE是矩形，再根据对角线相等即可解答；

(2)①根据线段中点的定义得到OE＝OC＝OD，根据三角形内角和得到∠DOE＝60°，继而得到结论；②延长CO交⊙O于G，连接DG交AB于P，则PC+PD的最小值＝DG，解直角三角形即可得到结论．

解：（1）连接OD，

∵⊙O的直径AB＝12，

∴圆的半径为12÷2＝6，

∵OC⊥AB，DE⊥OC，DF⊥AB，

∴四边形OFDE是矩形，

∴EF＝OD＝6；

（2）①∵点E为OC的中点，

∴OE＝OC＝OD，

∴∠EDO＝30°，

∴∠DOE＝60°，

∴弧CD的度数为60°；

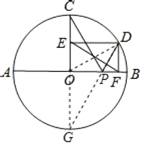
②延长CO交⊙O于G，连接DG交AB于P，

则PC+PD的最小值＝DG，

∵∠G＝∠COD＝30°，

∵EG＝9，

∴DG＝＝＝，

∴PC+PD的最小值为．