题目内容
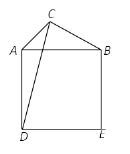
【题目】如图1,△ABC的AB边为圆O的弦,AC、BC分别交圆O于D、E,弧AD=弧BE,∠C=60°;

(1)求证:△ABC为等边三角形;
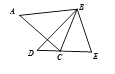
(2)如图2,F为弧AD上一点,连接FE并延长至G,连接BG,若∠AFB=∠G,求∠FBG的正弦值;
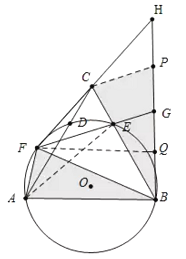
(3)如图3,在(2)的条件下,连接FC并延长交BG延长线于H,若CF=CH,AF=7,HG=12,求线段BF的长度。
【答案】(1)见解析;(2)sin∠FBG=![]() ;(3)BF=16
;(3)BF=16
【解析】
(1)由![]() 得到
得到![]() ,进而证明∠A=∠B即可解决问题;
,进而证明∠A=∠B即可解决问题;
(2)首先证明∠ABF=∠EBG,推出∠FBG=∠ABC=60°,根据特殊角三角函数值可得答案;
(3)如图3中,作CP∥FG,交BH于P,作FQ⊥BH于Q,连接AE,设BQ=x,首先证明△ABF≌△CBP,推出PC=AF=7,BF=PB,推出BF=BP=2BQ=2x,FQ=![]() x,GQ=2xx6=x6,在Rt△FGQ中,由FG2=FQ2+GQ2,列出方程即可解决问题.
x,GQ=2xx6=x6,在Rt△FGQ中,由FG2=FQ2+GQ2,列出方程即可解决问题.
(1)∵![]() ,
,
∴![]() ,
,
∴∠A=∠B,
∵∠C=60°,
∴∠A=∠B=∠C=60°,
∴△ABC是等边三角形.
(2)∵∠BEG+∠BEF=180°,∠BEF+∠FAB=180°,
∴∠BEG=∠BAF,
∵∠BEG+∠G+∠EBG=180°,∠AFB+∠FAB+∠ABF=180°,∠AFB=∠G,
∴∠ABF=∠EBG,
∴∠FBG=∠ABC=60°,
∴sin∠FBG=![]() ;
;
(3)如图,作CP∥FG,交BH于P,作FQ⊥BH于Q,连接AE,设BQ=x,
∵FC=CH,
∴HP=PG,
∴FG=2PC,∠FGB=∠CPB,
∵∠AFB=∠FGB,
∴∠AFB=∠CPB,
在△ABF和△CBP中,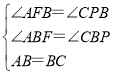 ,
,
∴△ABF≌△CBP,
∴PC=AF=7,BF=PB,
∴FG=14.
在Rt△FBQ 中,∵∠FQB=90°,∠FBQ=60°,
∴∠BFQ=30°,
∴BF=BP=2BQ=2x,FQ=![]() x,GQ=2xx6=x6,
x,GQ=2xx6=x6,
在Rt△FGQ中,∵FG2=FQ2+GQ2,
∴142=(x)2+(6x)2,
∴x=8或5(舍去),
∴BF=2x=16.


【题目】(问题提出)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有多少种不同的选择方法?
,有多少种不同的选择方法?
(问题探究)为发现规律,我们采用一般问题特殊化的策略,先从最简单的问题入手,再逐次递进,最后得出一般性的结论.
探究一:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,会有多少种不同的选择方法?
个连续的自然数,会有多少种不同的选择方法?
当![]() ,
,![]() 时,显然有
时,显然有![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有
时,有![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() 这
这![]() 种不同的选择方法;
种不同的选择方法;
![]()
当![]() ,
,![]() 时,有________种不同的选择方法;
时,有________种不同的选择方法;

……
由上可知:从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法.
个连续的自然数,有_______种不同的选择方法.
探究二:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个,
个,![]() 个……
个……![]()
![]() 个连续的自然数,分别有多少种不同的选择方法?
个连续的自然数,分别有多少种不同的选择方法?
我们借助下面的框图继续探究,发现规律并应用规律完成填空.
|
|
| ... |
|
|
|
|
|
|
|
|
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
从![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数,有_______种不同的选择方法;
个连续的自然数,有_______种不同的选择方法;
……
由上可知:如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]()
![]() 个连续的自然数,有______种不同的选择方法.
个连续的自然数,有______种不同的选择方法.
(问题解决)如果从![]() ,
,![]() 个连续的自然数中选择
个连续的自然数中选择![]() 个连续的自然数
个连续的自然数![]() ,有_______种不同的选择方法.
,有_______种不同的选择方法.
(实际应用)我们运用上面探究得到的结论,可以解决生活中的一些实际问题.
(1)今年国庆七天长假期间,小亮想参加某旅行社组织的青岛两日游,在出行日期上,他共有______种不同的选择.
(2)星期天,小明、小强和小华三个好朋友去电影院观看《我和我的祖国》,售票员李阿姨为他们提供了第七排![]() 号到
号到![]() 号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
号的电影票让他们选择,如果他们想拿三张连号票,则一共有______种不同的选择方法.
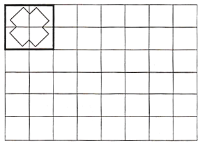
(拓展延伸)如图,将一个![]() 的图案放置在
的图案放置在![]() 的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
的方格纸中,使它恰好盖住其中的四个小正方形,共有______种不同的放置方法.
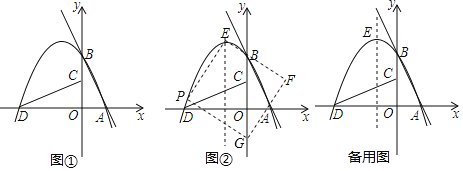
【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变最x和对应函数值y1,y2的部分对应值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时,自变量x的取值范图是_____.