题目内容
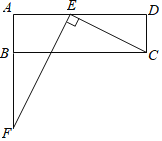
【题目】如图,Rt△ABC中,AC=CB,点E,F分别是AC,BC上的点,△CEF的外接圆交AB于点Q,D.
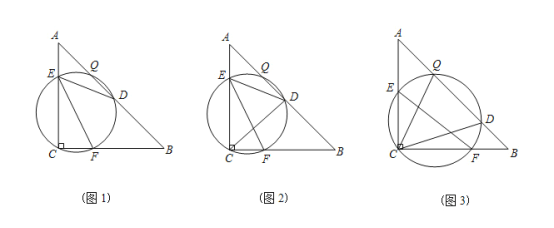
(1)如图1,若点D为AB的中点,求证:∠DEF=∠B;
(2)在(1)问的条件下:
①如图2,连结CD,交EF于H,AC=4,若△EHD为等腰三角形,求CF的长度.
②如图2,△AED与△ECF的面积之比是3:4,且ED=3,求△CED与△ECF的面积之比(直接写出答案).
(3)如图3,连接CQ,CD,若AE+BF=EF,求证:∠QCD=45°.
【答案】(1)见解析;(2)①0或2或4﹣2![]() ;②
;②![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)连结CD.根据圆周角定理解决问题即可.
(2)①分三种情形:如图2-1中,当EH=HD,可证四边形CFDE是正方形CF=2.如图2-2中,当EH=ED时,∠EDH=∠EHD=67.5°,如图2-3中,当DA=FH时,点E于A重合,点H与C重合,分别求解即可解决问题.
②如图2-4中,作DM⊥AC于M,DN⊥BC于N,连接DF.证明△ADE≌△CDF(SAS),推出AE=CF,S△ADE=S△CDF,由DC平分∠ACB,DM⊥AC,DN⊥BC,推出DM=DN,可得四边形DMCN是正方形,推出DM=CM=CN=DN,因为![]() =
=![]() =
=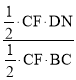 =
=![]() =
=![]() ,,所以可以假设DN=3k,EC=4k,则AC=BC=6k,AE=CF=2k,再利用三角形的面积公式计算机可解决问题.
,,所以可以假设DN=3k,EC=4k,则AC=BC=6k,AE=CF=2k,再利用三角形的面积公式计算机可解决问题.
(3)连接OD,OQ,作ER⊥AB,OH⊥AB,FK⊥AB.想办法证明△ODQ是等腰直角三角形即可解决问题.
(1)证明:连结CD.

在Rt△ABC中,∵AC=CB,
∴∠A=∠B=45°,
∵CD=DB,
∴∠DCB=∠B=45°,
∵∠DEF=∠DCB,
∴∠DEF=∠B.
(2)解:①如图2﹣1中,当EH=HD,可证四边形CFDE是正方形CF=2.
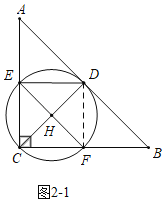
如图2﹣2中,当EH=ED时,∠EDH=∠EHD=67.5°,

∵∠EDF=∠CDB=90°,
∴∠EDH=∠BDF=67.5°,
∴∠BFD=180°﹣45°﹣67.5°=67.5°,
∴∠BDF=∠BFD,
∴BD=BF,
∵AC=BC=4,∠ACB=90°,
∴AB=![]() =4
=4![]() ,
,
∴BD=BF=2![]() ,
,
∴CF=4﹣2![]() .
.
如图2﹣3中,当DA=FH时,点E于A重合,点H与C重合,CF=0.
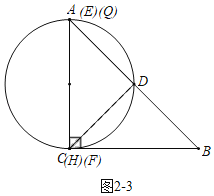
综上所述,满足条件的CF的值为0或2或4﹣2![]() .
.
②如图中,作DM⊥AC于M,DN⊥BC于N,连接DF.

∵CA=CB,AD=DB,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,CD=DA=DB
∴DE=DF,
∵∠ADC=∠EDF=90°,
∴∠ADE=∠CDF,
∴△ADE≌△CDF(SAS),
∴AE=CF,S△ADE=S△CDF,
∵DC平分∠ACB,DM⊥AC,DN⊥BC,
∴DM=DN,可得四边形DMCN是正方形,
∴DM=CM=CN=DN,
∵![]() =
=![]() =
=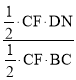 =
=![]() =
=![]() ,
,
∴可以假设DN=3k,EC=4k,则AC=BC=6k,AE=CF=2k,
∴![]() =
= =
=![]() .
.
(3)证明:连接OD,OQ,作ER⊥AB,OH⊥AB,FK⊥AB.

∵ER∥OH∥FK,EO=OF,
∴RH=HK
∴OH=![]() (ER+FK),
(ER+FK),
∵ER=![]() AE,FK=
AE,FK=![]() FB,
FB,
∴OH=![]() (AE+BF)=
(AE+BF)=![]() EF=
EF=![]() OE=
OE=![]() OQ,
OQ,
∴∠OQD=∠ODQ=45°,
∴∠QOD=90°,
∴∠QCD=45°.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
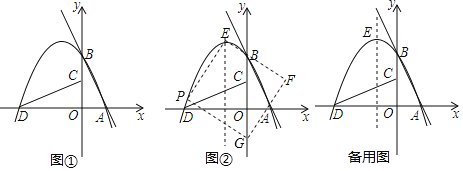
名师指导一卷通系列答案【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变最x和对应函数值y1,y2的部分对应值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时,自变量x的取值范图是_____.