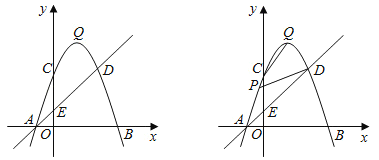题目内容
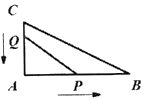
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行于⊙O的弦MB,连接DM并延长交x轴于点C.
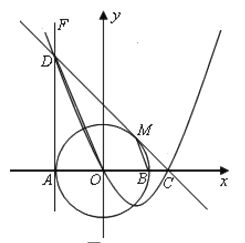
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求经过D、O、C三点的抛物线的解析式.
(3)若坐标平面内的点P,使得以点P和三点D、O、C为顶点的四边形是平行四边形,求P点的坐标.
【答案】(1)见解析;(2)y=![]() x2-
x2-![]() x;(3)P1(-
x;(3)P1(-![]() ,4),P2(
,4),P2(![]() ,4),P3(
,4),P3(![]() ,-4)
,-4)
【解析】
(1)连接OM,根据DO∥MB即可证得△AOD≌△MOD,从而得出∠OMD=∠OAD,因为DA⊥OA,即可得OM⊥CD;
(2) 设MC=x,可证得△OMC∽△DAC,利用相似三角形的性质得出OC=2x-2,利用勾股定理即可列出方程即可求解;
(3)要使以点P和三点D、O、C为顶点的四边形是平行四边形,则分三种情况讨论:①当DP∥OC,DC为对角线时,②当PD∥OC,DO为对角线时,③当DC∥OP,OC为对角线时,根据每种情况求解即可.
(1) 直线DC与⊙O相切.证明如下:
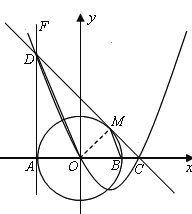
如图,连接OM,则OM=OB,
∴∠OMB=∠OBM.
∵DO∥MB,
∴∠AOD=∠OBM, ∠MOD=∠OMB,
∴∠AOD=∠MOD.
又∵OA=OM,OD=OD,
∴△AOD≌△MOD,
∴∠OMD=∠OAD.
而DA⊥OA,
∴∠OAD=90°,
∴∠OMD=90°,即OM⊥CD,
∴直线DC与⊙O相切.
(2)设MC=x.
∵∠OMC=∠DAC=90°,∠OCM=∠DCA,
∴△OMC∽△DAC,
∴![]() =
=![]() .
.
∵OM=OA=2,DA=4,AC=OA+OC=2+OC,
∴![]() =
=![]() ,
,
∴OC=2x-2.
在Rt△OMC中,
∵OM2+MC2=OC2,
∴22+x2=(2x-2)2,
解得x1=![]() ,x2=0(舍去),
,x2=0(舍去),
∴OC=2×![]() -2=
-2=![]() ,
,
∴C(![]() ,0).
,0).
因为抛物线经过坐标原点O,所以c=0,可设抛物线的解析式为y=ax2+bx,将(-2,![]() ,0)代入,得
,0)代入,得
 解之,得
解之,得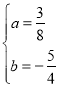 .
.
∴y=![]() x2-
x2-![]() x.
x.
(3)①当DP∥OC,DC为对角线时
∵D (-2,4),C(![]() ,0),
,0),
∴AO=OB=2,OC=![]()
∴P1(![]() ,4)
,4)
②当PD∥OC,DO为对角线时
∵DP2=OC=![]()
∴P2(-![]() ,4)
,4)
③当DC∥OP,OC为对角线时
同理可得P3(![]() ,-4).
,-4).
故P点坐标为:P1(![]() ,4),P2(-
,4),P2(-![]() ,4),P3(
,4),P3(![]() ,-4)
,-4)

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案