题目内容
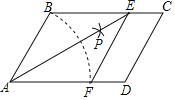
【题目】如图,在平行四边形ABCD中,以A为圆心,AB长为半径画弧交AD于点F;再分别以B、F为圆心,大于![]() 的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF是菱形.
的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF是菱形.
(1)求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为8,![]() ,求∠C的大小.
,求∠C的大小.
【答案】(1)证明见解析;(2)∠C=60°.
【解析】
(1)先证明△AEB≌△AEF,推出∠EAB=∠EAF,由AD∥BC,推出∠EAF=∠AEB=∠EAB,得到BE=AB=AF,由此即可证明;
(2)连结BF,交AE于G.根据菱形的性质得出AB=2,AG=![]() AE=
AE=![]() ,再根据三角函数解答即可.
,再根据三角函数解答即可.
解:(1)在△AEB和△AEF中,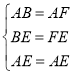 ,
,
∴△AEB≌△AEF(SSS),
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=BE,
∴四边形ABEF是菱形;
(2)如图,连结BF,交AE于G.
∵菱形ABEF的周长为8,
∴AB=![]() ×8=2
×8=2
∵AE⊥BF,![]()
∴GA=![]() AE=
AE=![]() ,
,
在Rt△AGB中,cos∠BAE=![]() =
=![]() ,
,
∴∠BAG=30°,
∴∠BAF=2∠BAG=60°,
∴在ABCD中,∠C=∠BAF=60°.

【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做些力所能及的家务.王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
频 数 | 20 | 25 | 30 | 15 | 10 |
(1)抽取样本的容量是 .
(2)根据表中数据补全图中的频数分布直方图
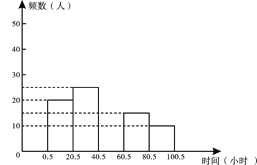
(3)样本的中位数所在时间段的范围是 .
(4)若该学校有学生1260人,那么大约有多少学生在寒假做家务的时间在40.5~100.5小时之间?