题目内容
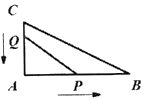
【题目】如图，在
中，∠A=90°，AB=12cm，AC=6cm，点P沿AB边从点A开始向点B以每秒2cm的速度移动，点Q沿CA边从点C开始向点A以每秒1cm的速度移动，P、Q同时出发，用t表示移动的时间．
（1）当t为何值时，△QAP为等腰直角三角形?
（2）当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似?
【答案】（1）
；（2）
或
．
【解析】
（1）利用距离=速度×时间可用含t的式子表示AP、CQ、QA的长，根据QA=AP列方程求出t值即可；
（2）分△QAP∽△BAC和△QAP∽△CAB两种情况，根据相似三角形的性质列方程分别求出t的值即可．
（1）∵点P的速度是每秒2cm，点Q的速度是每秒1cm，
∴
，
，
，
∵
时，
为等腰直角三角形，
∴
，
解得：
，
∴当时，为等腰直角三角形．
（2）根据题意，可分为两种情况，
①如图，当∽
时，
，
∴
，
解得：
，
②当∽
，
，
∴
，
解得：
，
综上所述：当或时，以点Q、A、P为顶点的三角形与
相似．
练习册系列答案
相关题目
