Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=![]() x2©Ā
x2©Ā![]() x©Ā9”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ń¨Ĺ”BC°ĘAC£ģ
x©Ā9”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ń¨Ĺ”BC°ĘAC£ģ
£®1£©«ůABļÕOCĶń≥§£Ľ
£®2£©Ķ„Eī”Ķ„A≥Ų∑Ę£¨—ōx÷ŠŌÚĶ„B‘ň∂Į£®Ķ„E”ŽĶ„A°ĘB≤Ľ÷ōļŌ£©£¨ĻżĶ„E◊ų÷ĪŌŖl∆Ĺ––BC£¨ĹĽAC”ŕĶ„D£ģ…ŤAEĶń≥§ő™m£¨°ųADEĶń√śĽżő™s£¨«ůsĻō”ŕmĶńļĮ żĻōŌĶ Ĺ£¨≤Ę–ī≥Ų◊‘ĪšŃŅmĶń»°÷Ķ∑∂őߣĽ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨Ń¨Ĺ”CE£¨«ů°ųCDE√śĽżĶń◊Óīů÷Ķ£Ľīň Ī£¨«ů≥Ų“‘Ķ„Eő™‘≤–ń£¨”ŽBCŌŗ«–Ķń‘≤Ķń√śĽż£®ĹŠĻŻĪ£Ń۶–£©£ģ

°ĺīūįł°Ņ£®1£©AB=9£¨OC=9£Ľ£®2£©s=![]() m2£®0£ľm£ľ9£©£Ľ£®3£©
m2£®0£ľm£ľ9£©£Ľ£®3£©![]() .
.
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©“—÷™Ň◊őÔŌŖĶńĹ‚őŲ Ĺ£¨ĶĪ![]() Ņ…»∑∂®
Ņ…»∑∂®![]() Ķ„◊ÝĪÍ£ĽĶĪ
Ķ„◊ÝĪÍ£ĽĶĪ![]() Ī£¨Ņ…»∑∂®
Ī£¨Ņ…»∑∂®![]() Ķ„Ķń◊ÝĪÍ£¨ĹÝ∂Ý»∑∂®
Ķ„Ķń◊ÝĪÍ£¨ĹÝ∂Ý»∑∂®![]() Ķń≥§£ģ
Ķń≥§£ģ
£®2£©÷ĪŌŖ![]() Ņ…Ķ√≥Ų
Ņ…Ķ√≥Ų![]() Ōŗň∆£¨ňŁ√«Ķń√śĽżĪ»Ķ»”ŕŌŗň∆Ī»Ķń∆Ĺ∑Ĺ£¨”…īňĶ√ĶĹĻō”ŕ
Ōŗň∆£¨ňŁ√«Ķń√śĽżĪ»Ķ»”ŕŌŗň∆Ī»Ķń∆Ĺ∑Ĺ£¨”…īňĶ√ĶĹĻō”ŕ![]() ĶńļĮ żĻōŌĶ Ĺ£Ľłýĺ›Ő‚ł…ŐűľĢ£ļĶ„
ĶńļĮ żĻōŌĶ Ĺ£Ľłýĺ›Ő‚ł…ŐűľĢ£ļĶ„![]() ”ŽĶ„
”ŽĶ„![]() ≤Ľ÷ōļŌ£¨Ņ…»∑∂®
≤Ľ÷ōļŌ£¨Ņ…»∑∂®![]() Ķń»°÷Ķ∑∂őߣģ
Ķń»°÷Ķ∑∂őߣģ
£®3£©ĘŔ ◊Ō»”√![]() Ń–≥Ų
Ń–≥Ų![]() Ķń√śĽżĪŪīÔ Ĺ£¨
Ķń√śĽżĪŪīÔ Ĺ£¨ ![]() Ķń√śĽż≤Óľīő™
Ķń√śĽż≤Óľīő™![]() Ķń√śĽż£¨”…īňŅ…Ķ√Ļō”ŕ
Ķń√śĽż£¨”…īňŅ…Ķ√Ļō”ŕ![]() ĶńļĮ żĻōŌĶ Ĺ£¨łýĺ›ļĮ żĶń–‘÷ Ņ…Ķ√ĶĹ
ĶńļĮ żĻōŌĶ Ĺ£¨łýĺ›ļĮ żĶń–‘÷ Ņ…Ķ√ĶĹ![]() Ķń◊Óīů√śĽż“‘ľįīň Ī
Ķń◊Óīů√śĽż“‘ľįīň Ī![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
ĘŕĻż![]() ◊Ų
◊Ų![]() ĶńīĻŌŖ
ĶńīĻŌŖ![]() £¨’‚łŲīĻŌŖ∂őĶń≥§ľīő™”Ž
£¨’‚łŲīĻŌŖ∂őĶń≥§ľīő™”Ž![]() Ōŗ«–Ķń
Ōŗ«–Ķń![]() ĶńįŽĺ∂£¨Ņ…łýĺ›Ōŗň∆»żĹ«–ő
ĶńįŽĺ∂£¨Ņ…łýĺ›Ōŗň∆»żĹ«–ő![]() Ķ√ĶĹĶńŌŗĻōĪ»ņżŌŖ∂ő«ůĶ√ł√įŽĺ∂Ķń÷Ķ£¨”…īňĶ√Ĺ‚£ģ
Ķ√ĶĹĶńŌŗĻōĪ»ņżŌŖ∂ő«ůĶ√ł√įŽĺ∂Ķń÷Ķ£¨”…īňĶ√Ĺ‚£ģ
‘Ő‚Ĺ‚őŲ£ļ(1)“—÷™£ļŇ◊őÔŌŖ![]()
ĶĪx=0 Ī,y=9,‘Ú£ļC(0,9)£Ľ
ĶĪy=0 Ī, ![]() ,Ķ√£ļ
,Ķ√£ļ ![]() ,‘Ú£ļA(3,0)°ĘB(6,0)£Ľ
,‘Ú£ļA(3,0)°ĘB(6,0)£Ľ
°ŗAB=9£¨OC=9.
(2) ![]()
°ŗ°ųAED°◊°ųABC£¨
 ľī£ļ
ľī£ļ 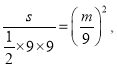 Ķ√£ļ
Ķ√£ļ ![]()

(3)Ĺ‚∑®“Ľ£ļ ![]()
![]()
°Ŗ0<m<9£¨
°ŗĶĪ![]() Ī,
Ī, ![]() »°Ķ√◊Óīů÷Ķ,◊Óīů÷Ķő™
»°Ķ√◊Óīů÷Ķ,◊Óīů÷Ķő™![]() īň Ī,
īň Ī, ![]()
ľ«E”ŽBCŌŗ«–”ŕĶ„M£¨Ń¨Ĺ”EM£¨‘ÚEM°ÕBC£¨…ŤEĶńįŽĺ∂ő™r.
‘ŕ![]() ÷–,
÷–, ![]()
![]()
°ŗ°ųBOC°◊°ųBME£¨
![]()

![]()
°ŗňý«ů![]() Ķń√śĽżő™£ļ
Ķń√śĽżő™£ļ 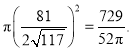

 –°—ßŅő Ī◊ų“Ķ»ęÕ®Ń∑įłŌĶŃ–īūįł
–°—ßŅő Ī◊ų“Ķ»ęÕ®Ń∑įłŌĶŃ–īūįł ĹūįśŅőŐ√Ņő Ī—ĶŃ∑ŌĶŃ–īūįł
ĹūįśŅőŐ√Ņő Ī—ĶŃ∑ŌĶŃ–īūįł Ķ•‘™»ęń‹Ń∑ŅľĺŪŌĶŃ–īūįł
Ķ•‘™»ęń‹Ń∑ŅľĺŪŌĶŃ–īūįł –¬Ľ∆ł‘ĪÝ∑®√‹ĺŪŌĶŃ–īūįł
–¬Ľ∆ł‘ĪÝ∑®√‹ĺŪŌĶŃ–īūįł




