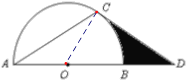
题目内容
【题目】如图，点
在
的直径
的延长线上，点
在
上， 
， 
，
（1）求证： 
是
的切线；
（2）若
的半径为2，求图中阴影部分的面积.
【答案】（1）证明见解析；（2）
.
【解析】试题分析：（1）连接OC．只需证明∠OCD＝90°．根据等腰三角形的性质即可证明；
（2）阴影部分的面积即为直角△OCD的面积减去扇形COB的面积．
试题解析：
（1）证明：连接OC，
∵AC＝CD，∠ACD＝120°，
∴∠CAD＝∠CDA＝30°，
∵OA＝OC，
∴∠CAD＝∠OCA＝30°，
∴∠COD＝60°
∴∠OCD＝90°，
∴CD是⊙O的切线；
（2）∵∠ACD＝30°，∠OCD＝90°，OC＝2，
在Rt△OCD中，
∵
＝tan60°，
∴CD＝2
，
S阴影＝S△COD－S扇形COB＝
.
练习册系列答案
相关题目
【题目】如图，
中，
，
，点P从顶点B出发，沿B→C→A以每秒1cm的速度匀速运动到A点，设运动时间为x秒，
长度为y cm．某学习小组对函数y随自变量x的变化而变化的规律进行了探究．下面是他们的探究过程，请补充完整：
（1）通过取点，画图，测量，得到了x（秒）与y（cm）的几组对应值：
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.2 | 3.6 | 3.2 | 3.0 | 3.6 | 4.2 | 5.0 |
要求：补全表格中相关数值（保留一位小数）；
（2）在平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当x约为__________时，
．