题目内容
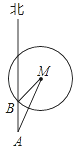
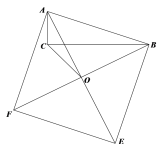
【题目】如图,以Rt![]() 的斜边AB为一边在
的斜边AB为一边在![]() 同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,
同侧作正方形ABEF.点O为AE与BF的交点,连接CO,若CA = 2,![]() ,那么四边形ABOC的面积为_______.
,那么四边形ABOC的面积为_______.
【答案】![]()
【解析】
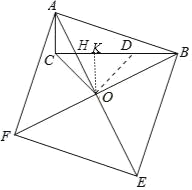
在BC上取一点D,使BD=AC=2,连接OD,可证得△BOD≌△AOC,得到OD=OC=![]() ,再得到△COD是等腰直角三角形,根据勾股定理求出CD,故得到BC的长,再求出△ABC,△BCO的面积即可.
,再得到△COD是等腰直角三角形,根据勾股定理求出CD,故得到BC的长,再求出△ABC,△BCO的面积即可.
如图,在BC上取一点D,使BD=AC=2,连接OD,作OK⊥BC于K,
∵∠CAO=90°-∠AHC,∠OBD=90°-∠OHB,
∵∠AHC=∠OHB,
∴∠CAO=∠OBD
∵四边形ABEF是正方形,
∴OA=OB, BD=AC
∴△BOD≌△AOC,
OD=OC=![]() ,∠BOD=∠AOC,
,∠BOD=∠AOC,
∵∠BOD+∠DOH=90°,
∴∠DOH+∠COA=90°,即∠COD=90°,
∴△COD是等腰直角三角形,
∴CD=![]() ,OK=
,OK=![]()
∴BC=![]()
∴四边形ABOC的面积=![]() =
=![]() =
=![]()
故填:![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某玩具厂计划一周生产某种玩具700件,平均每天生产100件,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -6 | +6 | -3 |
(1)根据记录的数据可知该厂星期四生产玩具 件;
(2)产量最多的一天比产量最少的一天多生产玩具 件;
(3)根据记录的数据可知该厂本周实际生产玩具 件;
(4)该厂实行每周计件工资制,每生产一件玩具可得20元,若超额完成任务,则超过部分每件另奖5元;少生产一件扣4元,那么该厂工人这一周的工资总额是多少元?