题目内容
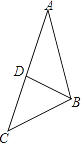
【题目】如图①,已知![]() 是
是![]() 的外角
的外角![]() 的平分线,且
的平分线,且![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() 恰好垂直平分
恰好垂直平分![]() ,求
,求![]() 的度数;
的度数;
(2)王涵探究后提出等式:![]() ,请通过证明判断“王涵发现”是否正确;
,请通过证明判断“王涵发现”是否正确;
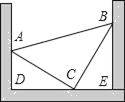
(3)如图②,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)60°(2)结论错误,理由见解析(3)80°.
【解析】
(1)根据垂直平分线的性质得到![]() ,
,![]() ,再根据角平分线的性质及平角的性质即可求解;
,再根据角平分线的性质及平角的性质即可求解;
(2)根据外角定理得到![]() ,根据角平分线的性质与平行线的判定定理可知
,根据角平分线的性质与平行线的判定定理可知![]() ,故结论错误;
,故结论错误;
(3)设![]() ,
,![]() ,根据已知条件和角平分线的性质与外角定理得到关于x,y的方程组即可求解x,y,故可得到
,根据已知条件和角平分线的性质与外角定理得到关于x,y的方程组即可求解x,y,故可得到![]() 的度数.
的度数.
(1)∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]()
则![]()
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∴![]() =
=![]()
又![]() +
+![]() =180°
=180°
∴![]() =60°
=60°
(2)结论错误;
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,
∴![]()
∵BE与CE相交,
∴![]()
∴![]()
故“王涵发现”错误;
(3)设![]() ,
,![]() ,
,
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
,
故![]()
∴![]()
∵![]()
∴![]() =2y
=2y
∴2x=3y①
∵![]()
∴![]()
故2x-y+y+x=90°②
由①②得x=30°,y=20°
∴![]() =80°.
=80°.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目