题目内容
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
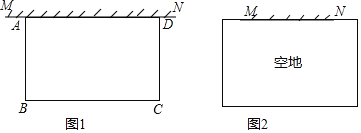
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
【答案】(1)利用旧墙AD的长为10米.(2)见解析.
【解析】
(1)按题意设出AD,表示AB构成方程;
(2)根据旧墙长度a和AD长度表示矩形菜园长和宽,注意分类讨论s与菜园边长之间的数量关系.
(1)设AD=x米,则AB=![]() 米
米
依题意得,![]() =450
=450
解得x1=10,x2=90
∵a=20,且x≤a
∴x=90舍去
∴利用旧墙AD的长为10米.
(2)设AD=x米,矩形ABCD的面积为S平方米
①如果按图一方案围成矩形菜园,依题意
得:
S=![]() ,0<x<a
,0<x<a
∵0<a<50
∴x<a<50时,S随x的增大而增大
当x=a时,S最大=50a-![]() a2
a2
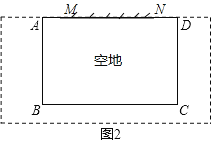
②如按图2方案围成矩形菜园,依题意得
S=![]() ,a≤x<50+
,a≤x<50+![]()
当a<25+![]() <50时,即0<a<
<50时,即0<a<![]() 时,
时,
则x=25+![]() 时,S最大=(25+
时,S最大=(25+![]() )2=
)2=![]() ,
,
当25+![]() ≤a,即
≤a,即![]() ≤a<50时,S随x的增大而减小
≤a<50时,S随x的增大而减小
∴x=a时,S最大=![]() =
=![]() ,
,
综合①②,当0<a<![]() 时,
时,![]() -(
-(![]() )=
)=![]() >0
>0
![]() >
>![]() ,此时,按图2方案围成矩形菜园面积最大,最大面积为
,此时,按图2方案围成矩形菜园面积最大,最大面积为![]() 平方米
平方米
当![]() ≤a<50时,两种方案围成的矩形菜园面积最大值相等.
≤a<50时,两种方案围成的矩形菜园面积最大值相等.
∴当0<a<![]() 时,围成长和宽均为(25+
时,围成长和宽均为(25+![]() )米的矩形菜园面积最大,最大面积为
)米的矩形菜园面积最大,最大面积为![]() 平方米;
平方米;
当![]() ≤a<50时,围成长为a米,宽为(50-
≤a<50时,围成长为a米,宽为(50-![]() )米的矩形菜园面积最大,最大面积为(
)米的矩形菜园面积最大,最大面积为(![]() )平方米.
)平方米.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目




