题目内容
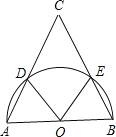
【题目】如图,已知点O为等腰三角形ABC的底边AB的中点,以点O为圆心,AB为直径的半圆分别交AC,BC于点D,E.
求证:(1)∠AOE=∠BOD;
(2)![]() .
.
【答案】证明见解析
【解析】(1)先画出图形,根据等腰三角形的性质,可得出∠A=∠B,再由OA=OD,OB=OE,可得出∠A=∠ODA,∠B=∠OEB,即可得出∠AOD=∠BOE,即可得出∠AOE=∠BOD;
(2)根据∠AOD=∠BOE,由弧、弦、圆心角之间的关系,即可得出![]() .
.
(1)∵CA=CB,
∴∠A=∠B,
∵OA=OD,OB=OE,
∴∠A=∠ODA,∠B=∠OEB,
∴∠AOD=∠BOE,
∴∠AOD+∠DOE=∠BOE+∠DOE,
∴∠AOE=∠BOD;
(2)∵∠AOD=∠BOE,
∴![]() .
.

练习册系列答案
相关题目