题目内容
【题目】如图,AB、CD 交于点 O,点 O 是线段 AB 和线段 CD 的中点.
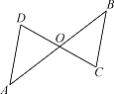
(1)求证:△AOD≌△BOC;
(2)求证:AD∥BC.
【答案】(1)见解析(2)见解析
【解析】
(1)由点O是线段AB和线段CD的中点可得出AO=BO,CO=DO,结合对顶角相等,即可利用全等三角形的判定定理(SAS)证出△AOD≌△BOC;
(2)结合全等三角形的性质可得出∠A=∠B,依据“内错角相等,两直线平行”即可证出结论.
证明:(1)∵点O是线段AB和线段CD的中点,
∴AO=BO,DO=CO.在△AOD和△BOC中,
AO=BO,∠AOD=∠BOC, CO=DO,
∴△AOD≌△BOC(SAS).
(2)∵由(1)知,△AOD≌△BOC,
∴∠A=∠B, ∴AD∥BC.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目