题目内容
【题目】如果三角形有一个内角为120°,且过某一顶点的直线能将该 三角形分成两个等腰三角形,那么这个三角形最小的内角度数是
A. 15°B. 40C. 15°或20°D. 15°或40°
【答案】C
【解析】
依据三角形的一个内角的度数为120°,且过某一顶点能将该三角形分成两个等腰三角形,运用分类思想和三角形内角和定理,即可得到该三角形其余两个内角的度数.
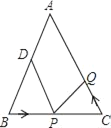
如图1,当∠A=120°,AD=AC,DB=DC时,∠ADC=∠ACD=30°,∠DBC=∠DCB=15°,
所以,∠DBC=15°,∠ACB=30°+15°=45°;
故∠ABC=60°,∠C=80°;
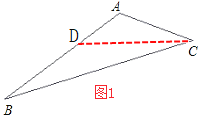
如图2,当∠BAC=120°,可以以A为顶点作∠BAD=20°,则∠DAC=100°,
∵△APB,△APC都是等腰三角形;
∴∠ABD=20°,∠ADC=∠ACD=40°,
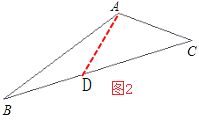
如图3,当∠BAC=120°,以A为顶点作∠BAD=80°,则∠DAC=40°,
∵△APB,△APC都是等腰三角形,
∴∠ABD=20°,∠ADC=100°,∠ACD=40°.
故选C.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目