题目内容
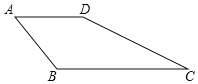
【题目】如图，在四边形ABCD中，AB=AD=6，∠A=60°，BC=10，CD=8．
（1）求∠ADC的度数；
（2）求四边形ABCD的面积．
【答案】（1）∠ADC=150°；（2）
．
【解析】
(1)连接BD,由题意可知△ABD是等边三角形求出∠ADB的度数,根据勾股定理的逆定理求出∠BDC的度数,即可求出∠ADC．
(2)将△ABD和△BDC的面积相加即可．
（1）连接BD．
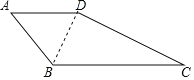
∵AB=AD=6,∠A=60°,
∴△ABD是等边三角形,
∴BD=6,∠ADB=60°．
∵BC=10,CD=8,
则BD2+CD2=82+62=100,BC2=102=100,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°；
（2）S=S△ABD+S△BDC
=
AD
AD+BDDC
=×6××6+×8×6
=9
+24．
练习册系列答案
相关题目
【题目】某中学举行“中国梦·校园好声音”歌手大赛，高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩（满分100）如下图所示：
根据图示信息，整理分析数据如下表：
平均数（分） | 中位数（分） | 众数（分） | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
（说明：图中虚线部分的间隔距离均相等）
（1）求出表格中
的值；
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较为稳定．
