题目内容
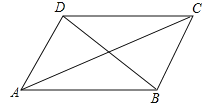
【题目】△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.

(1)如图1,若∠B=40°,∠C=62°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,求∠G的度数.
【答案】(1)∠DAE=11°;(2)∠DAE=![]() (∠C﹣∠B);说明见解析;(3)∠G=45°.
(∠C﹣∠B);说明见解析;(3)∠G=45°.
【解析】
(1)根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠DAE=∠DAC-∠EAC,即可得出;
(2)根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠DAE=∠DAC-∠EAC,即可得出;
(3)设∠ACB=α,根据角平分线的定义得到∠CAG=![]() ∠EAC=
∠EAC=![]() (90°-α)=45°-
(90°-α)=45°-![]() α,∠BCG=
α,∠BCG=![]() ∠BCF=
∠BCF=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,根据三角形的内角和即可得到结论.
α,根据三角形的内角和即可得到结论.
解:(1)∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,
∵AD是∠BAC的平分线,
∴∠DAC=![]() ∠BAC=39°,
∠BAC=39°,
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C=90°﹣62°=28°,
∴∠DAE=∠DAC﹣∠EAC=39°﹣28°=11°;
(2)∵∠BAC=180°﹣∠B﹣∠C,
∵AD是∠BAC的平分线,
∴∠DAC=![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵AE是BC边上的高,
在直角△AEC中,
∵∠EAC=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣![]() (∠B+∠C)﹣(90°﹣∠C)=
(∠B+∠C)﹣(90°﹣∠C)=![]() (∠C﹣∠B);
(∠C﹣∠B);
(3)设∠ACB=α,
∵AE⊥BC,
∴∠EAC=90°﹣α,∠BCF=180°﹣α,
∵∠CAE和∠BCF的角平分线交于点G,
∴∠CAG=![]() ∠EAC=
∠EAC=![]() (90°﹣α)=45°﹣
(90°﹣α)=45°﹣![]() α,
α,
∠BCG=![]() ∠BCF=
∠BCF=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠G=180°﹣∠GAC﹣∠ACG=180°﹣(45°﹣![]() α)﹣α﹣(90°﹣
α)﹣α﹣(90°﹣![]() α)=45°.
α)=45°.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案【题目】某超市第一次用6000元购进甲、乙两种商品,其中甲商品件数的2倍比乙商品件数的3倍多20件,甲、乙两种商品的进价和售价如下表(利润=售价﹣进价):
甲 | 乙 | |
进价(元/件) | 20 | 28 |
售价(元/件) | 26 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多560元,则第二次乙商品是按原价打几折销售的?
【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为;
(2)当y1>y2时,自变量x的取值范围是;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.