��Ŀ����
����Ŀ���������κ���y1=ax2+bx+c��һ�κ���y2=kx+m��ͼ��ʱ�����г��±���
x | �� | ��1 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y1 | �� | 0 | ��3 | ��4 | ��3 | 0 | 5 | 12 | �� |
y2 | �� | 0 | 2 | 4 | 6 | 8 | 10 | 12 | �� |
������ݱ�����Ϣ�ش��������⣬
��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ��
��2����y1��y2ʱ���Ա���x��ȡֵ��Χ����
��3����д�����κ���y1=ax2+bx+c��������ͬ�����ʣ�
���𰸡�
��1����0,��3��
��2����x����1��x��5ʱ,���κ�����ֵ����һ�κ�����ֵ
��3���⣺�ú�����ͼ�����ϣ���x=1ʱ�����������ֵ����x��1ʱ��y��x���������С����x��1ʱ��y��x�����������������Ϊ��1����4�����Գ���Ϊֱ��x=1��
����������1����x=0�����y����ֵ��ȷ����y�ύ�����꼴�ɣ���2�������ô���ϵ����������κ�����һ�κ����Ľ���ʽ�����������ͼ��Ľ��㣬�����ɵó����ۣ���3�����ö��κ��������ʣ����ڷ��Գ��ᣬ������ֱ�ӵó��𰸼��ɣ�
�⣺��1�����κ���y1=ax2+bx+c��ͼ����y�ύ������Ϊ��0����3������2��������ã�
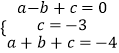 ��
��
���  ��
��
����κ����Ľ���ʽΪy=x2��2x��3=��x��1��2��4��
��һ�κ���y2=kx+m��ͼ����㣨��1��0������0��2����
�� ![]() ��
��
��� ![]() ��
��
��һ�κ����Ľ���ʽΪy=2x+2��
��ͼ��ʾ��
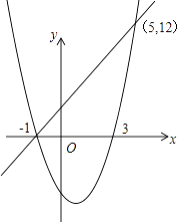
��x����1��x��5ʱ�����κ�����ֵ����һ�κ�����ֵ��
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

����Ŀ���ţ�2������֯��һ���ʶ��������ס������Ӹ�10�˵ı����ɼ���10���ƣ����±�����λ���֣���
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
��1���ӳɼ�����λ�����֣��Ҷӳɼ����������֣�
��2�������Ҷӳɼ���ƽ�����ͷ��
��3����֪�ӳɼ��ķ�����1.4��2 �� ��ɼ���Ϊ��������ӣ�
����Ŀ������ʦΪ�˴�ƽʱ�ڰ༶����ѧ�Ƚ�����ļס�����λͬѧ��ѡ��һ�˲μ���ȫ��������ѧϣ����������������λͬѧ�����˸��������ڸ����ڼ������5�β��飬��λͬѧ����ɼ��÷������ͼ��ʾ��
���ñ����ṩ�����ݣ�����������⣺
��1��������ͼ�ֱ�д���ס�����εijɼ���
�ף��� �����ң��� ����
��2����д����±���
ƽ���ɼ� | ��λ�� | ���� | ���� | |
�� | �� | 4 | ||
�� | 13 |
��3����������������Ϣ��������ѧ��ͳ��֪ʶ����������ʦ����ѡ����Ҫ˵�����ɣ�